The post-stack velocity continuation process is governed by a partial differential equation in the domain, composed by the seismic image coordinates (midpoint x and vertical time t) and the additional velocity coordinate v. Neglecting some amplitude-correcting terms (), the equation takes the form ()
| |
(82) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is linear and belongs to the hyperbolic type. It
describes a wave-type process with the velocity v acting as a
``time-like'' variable. Each constant-v slice of the function
P(x,t,v) corresponds to an image with the corresponding constant
velocity. The necessary boundary and initial conditions are
) is linear and belongs to the hyperbolic type. It
describes a wave-type process with the velocity v acting as a
``time-like'' variable. Each constant-v slice of the function
P(x,t,v) corresponds to an image with the corresponding constant
velocity. The necessary boundary and initial conditions are
| |
(83) |
Mathematically, equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) define a
Goursat-type problem (). Its analytical solution can be
constructed by a variation of the Riemann method in the form of an
integral operator (, ):
) define a
Goursat-type problem (). Its analytical solution can be
constructed by a variation of the Riemann method in the form of an
integral operator (, ):
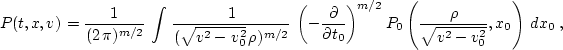 |
(84) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is equivalent (up to the
amplitude weighting) to conventional Kirchoff time migration
(). Similarly, in the frequency-wavenumber
domain, velocity continuation takes the form
) is equivalent (up to the
amplitude weighting) to conventional Kirchoff time migration
(). Similarly, in the frequency-wavenumber
domain, velocity continuation takes the form
| |
(85) |
If our task is to create many constant-velocity slices, there are
other ways to construct the solution of problem (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Two alternative spectral approaches are discussed in the next two
sections.
).
Two alternative spectral approaches are discussed in the next two
sections.