Solving the eikonal equation on a triangulated grid

Unstructured (triangulated) grids have computational advantages over rectangular ones in three common situations:

• When the number of grid points can be substantially reduced by putting them on an irregular grid. This situation corresponds to irregular distribution of details in the propagation medium.
• When the computational domain has irregular boundaries. One possible kind of boundary corresponds to geological interfaces and seismic reflector surfaces Wiggins et al. (1993). Another type of irregular boundary, in application to traveltime computations, is that of seismic rays. The method of bounding the numerical eikonal solution by ray envelopes has been introduced recently by Abgrall and Benamou (1996).
• When the grid itself needs to be dynamically updated to maintain a certain level of accuracy in the computation.

With its computational speed and unconditional stability, the fast marching method provides considerable savings in comparison with alternative, more accurate methods, such as semi-analytical ray tracing Guiziou et al. (1991); Stankovic and Albertin (1995) or the general Hamilton-Jacobi solver of Abgrall (1996).

 

test
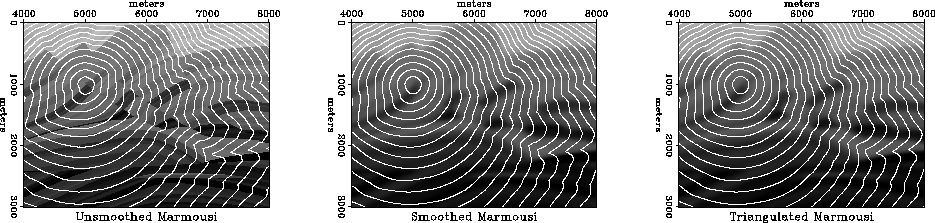
Figure 5 Traveltime contours, computed in the rough Marmousi model (left), the smoothed Marmousi (middle), and the smoothed triangulated Marmousi (right).

Figure 5 shows a comparison between first-arrival traveltime computations in regularly gridded and triangulated Marmousi models. The two results match each other within the first-order accuracy of the fast marching method. However, the cost of the triangulated computation has been greatly reduced by constraining the number of nodes.

Computational aspects of triangular grid generation are outlined in Appendix A. A three-dimensional application would follow the same algorithmic patterns.