Helix and multidimensional deconvolution

The major obstacle of applying an implicit extrapolation in three dimensions is that the inverted matrix is no longer tridiagonal. If we approximate the second derivative (Laplacian) on the 2-D plane with the commonly used five-point filter Z_x^-1 + Z_y^-1 -4 + Z_x + Z_y, then the matrix on the left side of equation (14), under the usual mapping of vectors from a two-dimensional mesh to one dimension, takes the infamous blocked-tridiagonal form Birkhoff (1971)  

$$\tilde{\bold{A}} = \left(\bold{I} -c\,\bold{D}_2\right) = ... ... & & & & -c_{n} \,\bold{I} & \bold{A}_n \end{array}\right]\;.$$ (17)

Inspecting this form more closely, we see that the main diagonal of $\tilde{\bold{A}}$, as well as the two offset diagonals formed by the scaled identity matrices, remains continuous, while the second top and bottom diagonals are broken. Therefore, even for constant c, the inverted matrix does not have a simple convolutional structure, and the cost of its inversion grows nonlinearly with the number of grid points.

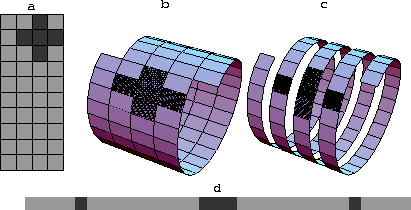
A helix transform , recently proposed by one of the authors Claerbout (1997a), sheds new light on this old problem. Let us assume that the extrapolation filter is applied by sliding it along the x direction in the $\{x,y\}$ plane. The diagonal discontinuities in matrix $\tilde{\bold{A}}$ occur exactly in the places where the forward leg of the filter slides outside the computational domain. Let's imagine a situation, where the leg of the filter that went to the end of the x column, would immediately appear at the beginning of the next column. This situation defines a different mapping from two computational dimensions to the one dimension of linear algebra. The mapping can be understood as the helix transform, illustrated in Figure 4 and explained in detail by Claerbout (1997a). According to this transform, we replace the original two-dimensional filter with a long one-dimensional filter. The new filter is partially filled with zero values (corresponding to the back side of the helix), which can be safely ignored in the convolutional computation.

 

helix
Figure 4 The helix transform of two-dimensional filters to one dimension. The two-dimensional filter in the left plot is equivalent to the one-dimensional filter in the right plot, assuming that a shifted periodic condition is imposed on one of the axes.

This is exactly the helix transform that is required to make all the diagonals of matrix $\tilde{\bold{A}}$ continuous. In the case of laterally invariant coefficients, the matrix becomes strictly Toeplitz (having constant values along the diagonals) and represents a one-dimensional convolution on the helix surface. Moreover, this simplified matrix structure applies equally well to larger second-derivative filters ( such as those described in Appendix B), with the obvious increase of the number of Toeplitz diagonals. Inverting matrix $\tilde{\bold{A}}$ becomes once again a simple inverse filtering problem. To decompose the 2-D filter into a pair consisting of a causal minimum-phase filter and its adjoint, we can apply spectral factorization methods from the 1-D filtering theory Claerbout (1976, 1992), for example, Kolmogorov's highly efficient method Kolmogorov (1939). Thus, in the case of a laterally invariant implicit extrapolation, matrix inversion reduces to a simple and efficient recursive filtering, which we need to run twice: first in the forward mode, and second in the adjoint mode.

 

heat3d
Figure 5 Heat extrapolation in two dimensions, computed by an implicit scheme with helix recursive filtering. The left plot shows the input temperature distributions; the two other plots, the extrapolation result at different time steps. The coefficient a is 2.

Figure 5 shows the result of applying the helix transform to an implicit heat extrapolation of a two-dimensional temperature distribution. The unconditional stability properties are nicely preserved, which can be verified by examining the plot of changes in the average temperature (Figure 6).

 

heat-mean Figure 6 Demonstration of the stability of implicit extrapolation. The solid curve shows the normalized mean temperature, which remains nearly constant throughout the extrapolation time. The dashed curve shows the normalized maximum value, which exhibits the expected Gaussian shape.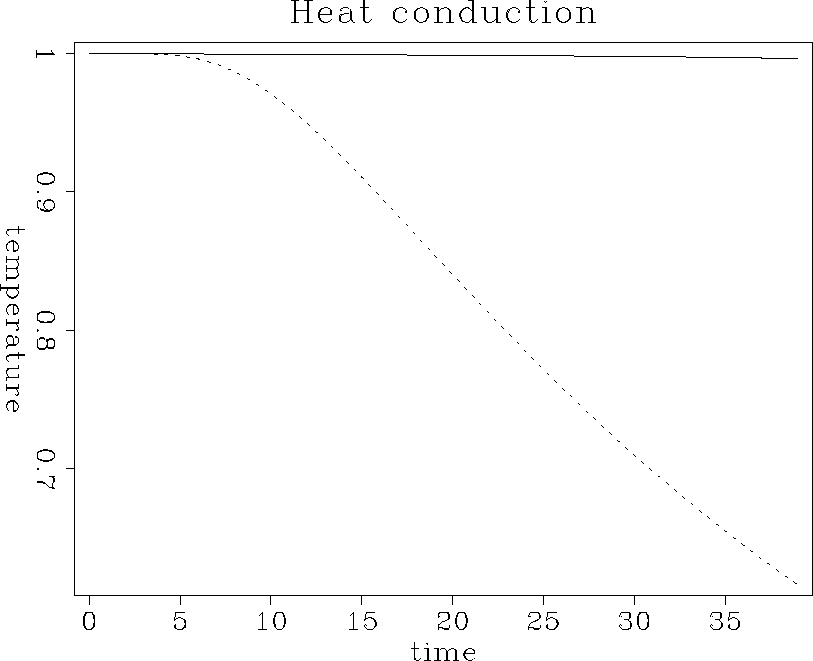

In principle, we could also treat the case of a laterally invariant coefficient with the help of the Fourier transform. Under what circumstances does the helix approach have an advantage over Fourier methods? One possible situation corresponds to a very large input data size with a relatively small extrapolation filter. In this case, the O(N log N) cost of the fast Fourier transform is comparable with the O(N_f N) cost of the space-domain deconvolution (where N corresponds to the data size, and N_f is the filter size). Another situation is when the boundary conditions of the problem have an essential lateral variation. The latter case may occur in applications of velocity continuation, which we discuss in the next section. Later in this paper, we return to the discussion of problems associated with lateral variations.