Next: Discussion
Up: Fomel, et al.: Interpolation
Previous: Theory of missing data
The first two examples in this paper are taken directly from
Geophysical Exploration Mapping Claerbout (1997). They
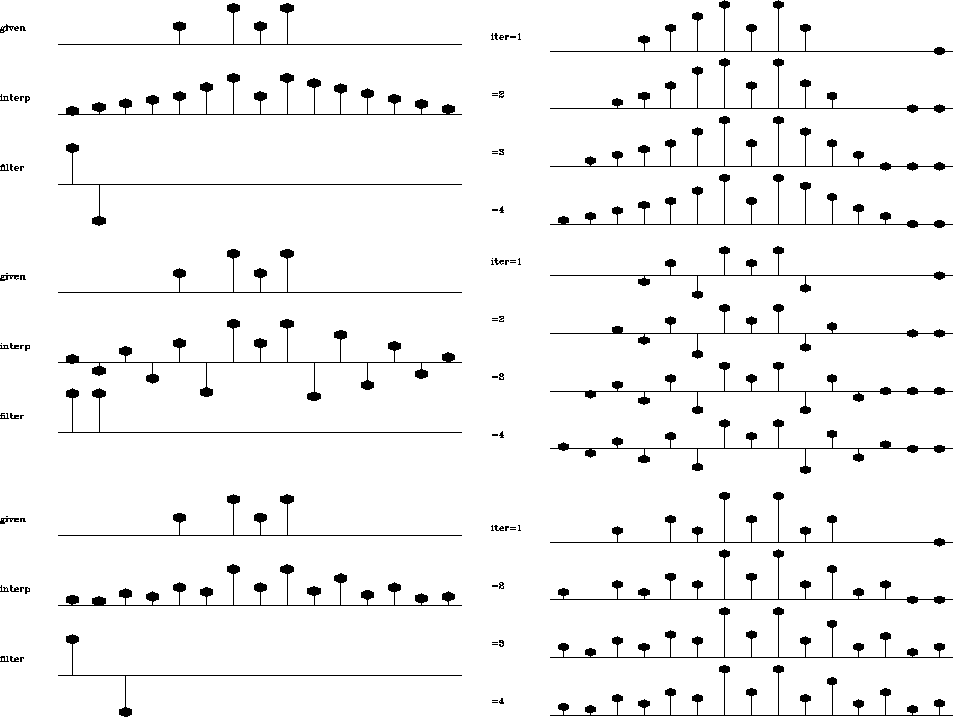
start from a simple 1-D synthetic data test. Figure 1
shows the interpolation results of the unpreconditioned technique with
three different filters. For comparison with the preconditioned
scheme, we changed the boundary convolution conditions from internal
to truncated transient convolution. The system was solved with a
conjugate-gradient iterative optimization.
mall
Figure 1 Unpreconditioned
interpolation with three different regularization filters. On the
left plot: the top shows the input data; the middle, the result of
interpolation; and the bottom, the filter. The right plot shows the
convergence process for the first four iterations.





As depicted on the right side of the figures, the interpolation
process starts with a ``complicated'' model and slowly ``simplifies''
it until the final result is achieved.
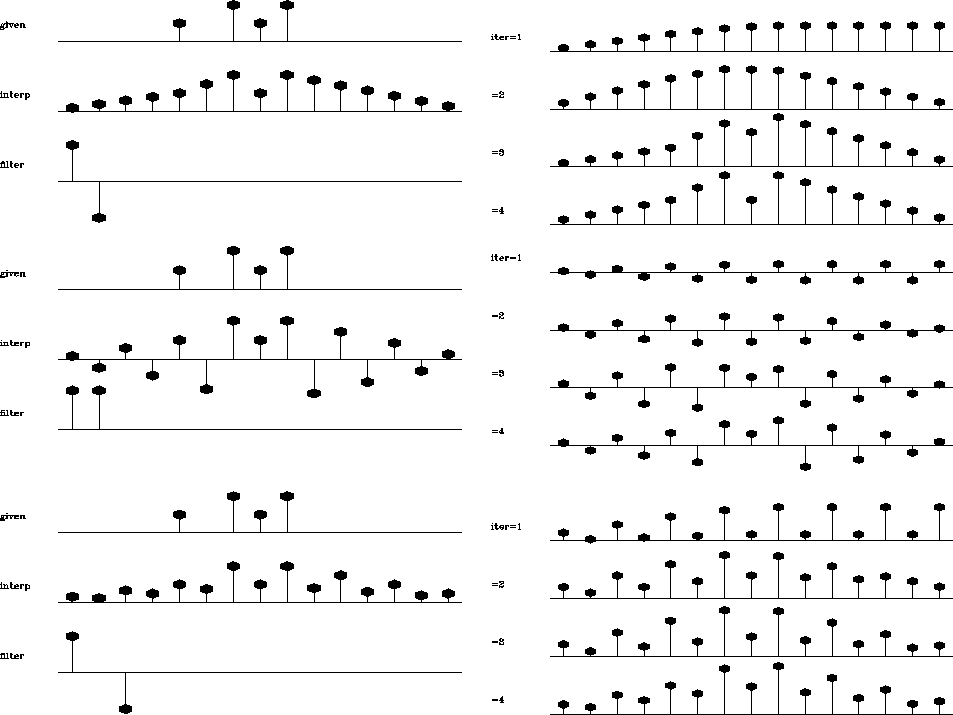
Preconditioned interpolation (Figure 2) behaves
differently. At the early iterations, the model is simple. As the
iteration proceeds, new details are added into the model.
After a surprisingly small number of iterations, the output closely
resembles the final output. This observation is fully consistent with
the general theory of regularization and preconditioning
Fomel (1997); Harlan (1995); Nichols (1994). The
final output of interpolation with recursive deconvolution
preconditioning is exactly the same as that of the original method.
sall
Figure 2 Interpolation with
preconditioning. On the left plot: the top shows the input data; the
middle, the result of interpolation; and the bottom, the filter. The
right plot shows the convergence process for the first four
iterations.





The next example is the SeaBeam dataset, a result of water bottom
measurements from a single day of acquisition. This dataset has been
used at SEP for benchmarking different strategies of data
interpolation. The left plot in Figure 3 shows the
original data. The right plot shows the result of (unpreconditioned)
missing data interpolation with the Laplacian filter. The result is
unsatisfactory, because the Laplacian filter doesn't absorb the
spatial frequency distribution of the input dataset. We judge the
quality of an interpolation scheme by its ability to hide the
footprints of the acquisition geometry in the final result.
seabdat
Figure 3 On the left, the
SeaBeam data: the depth of the ocean under ship tracks; on the
right, an interpolation with the Laplacian filter.





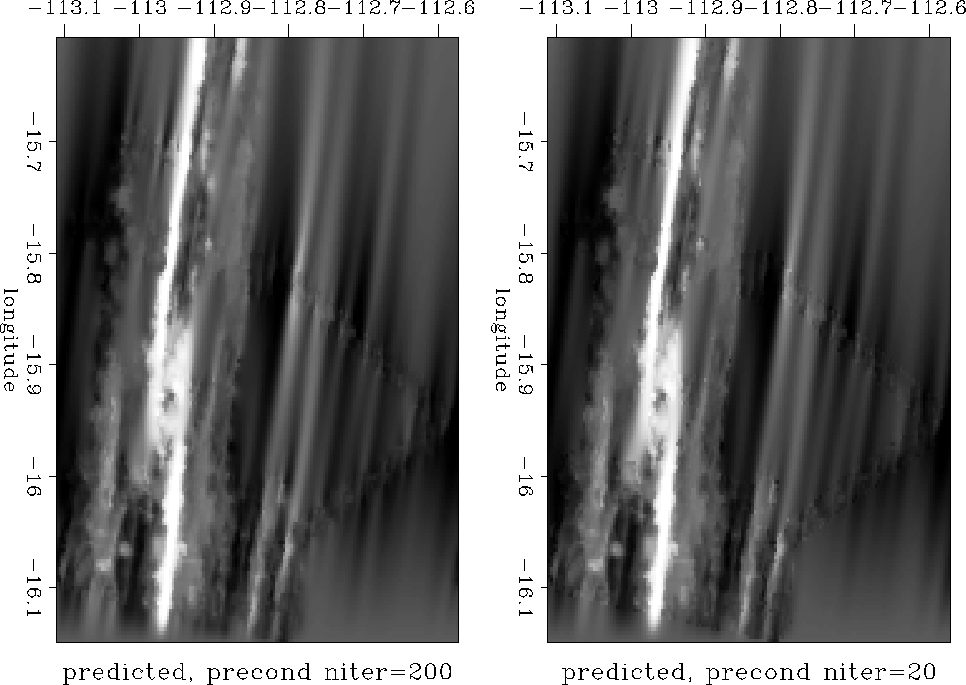
Claerbout (1997) obtains a significantly better result
(Figure 4) by replacing the Laplacian filter with a
prediction-error filter (PEF), estimated from the input data.
The result in the left plot of Figure 4 was obtained
after 200 conjugate-gradient iterations. If we stop after 20
iterations, the output (the right plot in Figure 4)
shows only a small deviation from the input data. Large areas of the
image remain unfilled.
seabold
Figure 4 SeaBeam interpolation
with the prediction-error filter. The left plot was taken after 200
conjugate-gradient iterations; the right, after 20 iterations.





Inverting the PEF convolution with the help of the helix transform, we
can now apply the inverse filtering operator to precondition the
interpolation problem. As expected, the result after 200 iterations
(the left plot in Figure 5) is similar to the result
of the corresponding unpreconditioned interpolation. However, the
output after just 20 iterations (the right plot in Figure 5)
is already fairly close to the solution.
seabnew
Figure 5 SeaBeam interpolation
with the inverse prediction-error filter. The left plot was taken after 200
conjugate-gradient iterations; the right, after 20 iterations.





For our third example we apply the preconditioning methodology to
simulate interpolating well log velocities using reflector dip
information as a guide. In the first two cases we used a
space-invariant filter for our operator 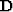 , and the
corresponding inverse
, and the
corresponding inverse 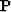 . In this example D is composed of
a series of steering filters, small plane wave anihilators, oriented at
some a priori angleClapp et al. (1997).
. In this example D is composed of
a series of steering filters, small plane wave anihilators, oriented at
some a priori angleClapp et al. (1997).
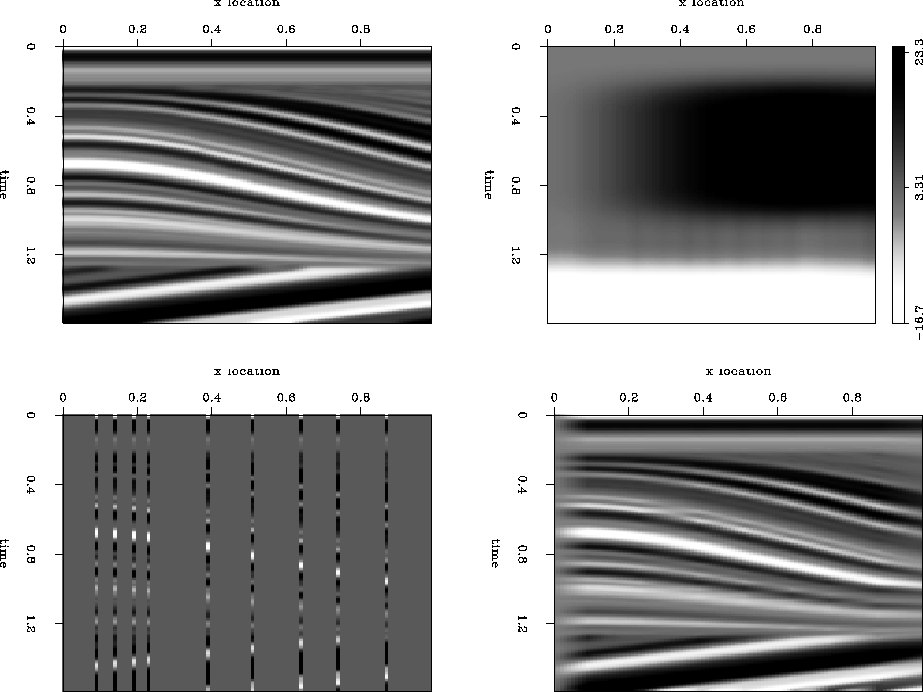
We started with a velocity field from a synthetic anticline model
above a horizontal unconformity. To build the steering filters we
make the assumption that velocity follows reflector dips. We first
select four reflectors that characterize dip in the section (Figure
qdome-combo1, top right). The selected dips are then
interpolated to all model locations and smoothed (Figure
qdome-combo1, top left). Using this dip field, the methodology
in equation (6), and a series of well logs (Figure qdome-combo1,
bottom left) constructed from the original velocity model, we
attempted to reinterpolate the unknown velocities. The bottom right
plot of Figure qdome-combo1 shows that the interpolation was
successful in minimal iterations (in this case only 12 iterations were
required).
qdome-combo1
Figure 6 Interpolating a synthetic
velocity field from the well data. The left top plot shows the
synthetic model; top right, the dip field for calculating steering
filters; bottom left, the input data; bottom right, the interpolation
result. Only 12 conjugate-gradient interpolations were required.










Next: Discussion
Up: Fomel, et al.: Interpolation
Previous: Theory of missing data
Stanford Exploration Project
10/9/1997