Carefully chosen tapers reduce leakage by replacing the
Fej![]() r kernel with kernels possessing smaller
side-lobes.
Note, however, the variance-bias tradeoff. Reducing the broad-band
bias (reducing the side-lobes of the kernel) amounts to increasing
the variance and the local bias (increasing the central lobe of the
kernel). A good spectral estimate should have both small bias and
small variance. This is where multitapering, K greater than 1,
proves to be
helpful. Combining several eigenspectrum estimates with good bias
properties preserves the small bias and reduces the variance of the
resulting multitaper spectral estimate. If the tapers are
mutually orthogonal, then, under the conditions of Theorem 4.4.2 of
Brillinger (1981b), their Fourier transforms will be asymptotically
independent zero-mean normal variates, so that the sum of the
eigenspectra will be asymptotically distributed as a
r kernel with kernels possessing smaller
side-lobes.
Note, however, the variance-bias tradeoff. Reducing the broad-band
bias (reducing the side-lobes of the kernel) amounts to increasing
the variance and the local bias (increasing the central lobe of the
kernel). A good spectral estimate should have both small bias and
small variance. This is where multitapering, K greater than 1,
proves to be
helpful. Combining several eigenspectrum estimates with good bias
properties preserves the small bias and reduces the variance of the
resulting multitaper spectral estimate. If the tapers are
mutually orthogonal, then, under the conditions of Theorem 4.4.2 of
Brillinger (1981b), their Fourier transforms will be asymptotically
independent zero-mean normal variates, so that the sum of the
eigenspectra will be asymptotically distributed as a ![]() variable.
Confidence intervals can then be easily constructed for the
multitapered spectral estimate. Internal measures of variability
such as the jackknife, free of any distributional assumptions, were
proposed in the literature by Thomson and Chave 1991 as alternative ways to
calculating variance estimates of the multitaper spectrum estimate.
References to nonparametric spectral estimation include Brillinger (1981a),
Brillinger (1981b), and Percival and Walden 1993.
variable.
Confidence intervals can then be easily constructed for the
multitapered spectral estimate. Internal measures of variability
such as the jackknife, free of any distributional assumptions, were
proposed in the literature by Thomson and Chave 1991 as alternative ways to
calculating variance estimates of the multitaper spectrum estimate.
References to nonparametric spectral estimation include Brillinger (1981a),
Brillinger (1981b), and Percival and Walden 1993.
The Generalized Sinusoidal Tapers
An orthogonal taper family based on sinusoids that requires little
computational effort is proposed by Riedel and Sidorenko 1995. Those
tapers are approximations to the so-called minimum bias tapers, also
proposed by Reidel and Sidorenko 1995, as a family with good
variance and bias properties, and therefore as excellent candidate for
multitapering data with no gaps in the observations. The GONG data
however, like any other helioseismic data, contain occasional missing
observations. Define the gap structure ![]() as the sequence of indicators specifying whether the
observation at time t is available. The case that all the
realizations are available corresponds to It = 1 for all
as the sequence of indicators specifying whether the
observation at time t is available. The case that all the
realizations are available corresponds to It = 1 for all ![]() . The generalized sinusoidal taper family
has K sequences of length T as members:
. The generalized sinusoidal taper family
has K sequences of length T as members:
![]() , k = 0, ... ,
K-1, the k-th order generalized sine taper
, k = 0, ... ,
K-1, the k-th order generalized sine taper ![]() ,being:
,being:
![]()
with
![]()
The orthogonality of the sine tapers is not necessarily preserved by the above operation. To obtain the final version of the generalized sine tapers, an additional step of re-orthogonalization is needed. Figure 11 shows the first two generalized sine tapers corresponding to the GONG Month 10 gap structure.
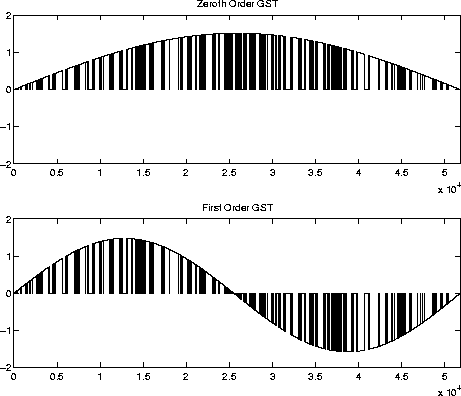 |
PARAMETRIC AND NON-PARAMETRIC SPECTRUM ESTIMATES
Figure 12 presents the parametric AR(99) and the nonparametric 100 sine tapered spectrum estimates. There is little difference between the two very differently obtained estimates! Both of them recover the overall shape of the underlying process and the 13 peaks at the generating frequencies. Note that the multitapered estimate is almost as smooth as the AR(99) estimate, particularly in the region of the peaks. In the region away from the generating frequencies, the multitapered estimate is slightly rougher than the smooth AR(99) estimate, but it is remarkable how similar in shape they are. It is certainly very encouraging that two fundamentally different methods produce spectrum estimates that are so alike, both close to the true spectrum. Does it follow that spectrum estimation via multitapering and via AR modeling are exchangeable? To answer that question, it is necessary to investigate the assumptions of the two procedures.
 |
First, there is a fundamental ``philosophical'' difference: the multitapering method is completely free of distributional assumptions, while the AR method assumes a certain functional form for the spectral density to be estimated. If there is prior knowledge that the data under investigation is a realization of an AR process, then assuming an AR model does make sense. The nonparametric multitapering method can be used in the absence of any distributional assumptions, whenever the spectrum of interest has a large dynamic range. As any continuous spectrum can be approximated by a long enough AR process, AR modeling can be used to estimate the spectrum of such process, but care must be exercised in determining the order of the model and in quantifying the goodness of the fit.
Second, the multitapering and the AR approaches have different free parameters: The number of tapers in the multitapering method, and the order of the AR process in the AR modeling. How to select the optimal number of tapers to use is a classical variance-bias trade-off problem that can be quantified Percival and Walden (1993): Increasing the number of tapers amounts to decreasing the variability, decreasing the broad-band bias due to power leakage, and increasing the local bias. The more tapers used, the smoother the resulting spectrum estimate is. Picking the order based on a realization of an assumed AR process is of different nature: Any estimated AR spectrum is smooth by definition; the order determines the details of the estimate. If too low of an order is selected, structure in the underlying spectral distribution might be missed, if too high an order is selected, spurious peaks might be introduced in the estimate.
Third, the bias and the standard error of the multitapered spectrum estimate can be obtained using the jackknife technique. Discussed in detail by Efron and Tibshirani 1993, this statistical procedure provides an empirical way, completely free of any distributional assumptions, to estimate the variability of the multitapered estimate. Essentially, if there are K tapers, a multitapered estimate based on K-1 tapers is computed K times, each time leaving one taper out. Then, the properly scaled standard error of those K ``leave-one-out'' estimates provides an estimate of the standard error of the K multitapered spectrum estimate. Traditional variability estimates, both for the multitapered and for the AR methods, rely on distributional assumptions and asymptotics.
Fourth, the issue of missing data needs to be addressed in the AR
modeling. The AR estimation algorithms used in this paper assume
the data values of zero whenever there were gaps in the GONG Month 10
series. The codes need to be adjusted to deal with this issue
properly. The tapers, on the other hand, were specifically designed
to take Month 10's gap structure into account, and therefore are
constrained to be zero at the locations of the missing values - see
Figure 11. Note that other orthogonal taper families,
such as the discrete prolate spheroidal sequences proposed by
Thomson 1982, and discussed in detail by
Percival and Walden 1993,
and the minimum bias tapers proposed by Riedel and Sidorenko 1995, and
their generalized versions for data with missing observations do
exist. The former depend on the bandwidth parameter W, ![]() ,and are the vectors with maximal energy concentration in the frequency
band [-W, W], designed to suppress power leakage from the resonant
modes. The latter minimize the local bias, defined as the integral
of the product of frequency squared times energy at that frequency.
,and are the vectors with maximal energy concentration in the frequency
band [-W, W], designed to suppress power leakage from the resonant
modes. The latter minimize the local bias, defined as the integral
of the product of frequency squared times energy at that frequency.
Finally, the computational complexity of calculating the general sine multitapered estimate and calculating the AR estimate is comparable. Because of the closed form expression of the sine tapers, they can be evaluated almost instantly even for very long datasets. The additional step of reorthogonalization in the missing values case does not significantly increase the calculation time. Calculating K of the ``best'' prolate or minimum bias tapers however, amounts to solving for the K largest eigenvalues and associated eigenvectors of a T by T matrix, where T is the length of the series. Using the block Lanczos algorithm Parlett (1980) with reorthogonalization, and special algorithms that exploit the Toeplitz structure of the large matrices, the running time to obtain 100 tapers, each of length T=51840, takes more than 200 hours on a Sun Sparc Ultra 2 machine. Computationally, therefore, the cost of getting the prolate or the minimum bias tapers and then calculating the multitapered estimate with those tapers is higher than calculating the AR spectrum estimate.
In conclusion, the autoregressive and the generalized sine multitaper spectral analysis of the solar oscillations data considered in this paper result in very comparable estimates. Based on the simulation data, where the location of the modes is known, it is determined that both methods recover the true structure of the spectrum. The spectrum of the observed data thus might be estimated using either methods, provided that the process that generates the GONG data resembles the process underlying the synthetic data. It is up to the investigator to know the advantages and limitations of both methods, and to make an informed decision about which method to use.