![]()
where ![]() is the identity matrix.
We have the preconditioning operator
is the identity matrix.
We have the preconditioning operator ![]() , which applies polynomial
division using the helix methodology. In this case we have a
single equation in our estimation problem,
, which applies polynomial
division using the helix methodology. In this case we have a
single equation in our estimation problem,
| |
(18) |
For this experiment
we create a series of well logs by subsampling a 2-D velocity field.
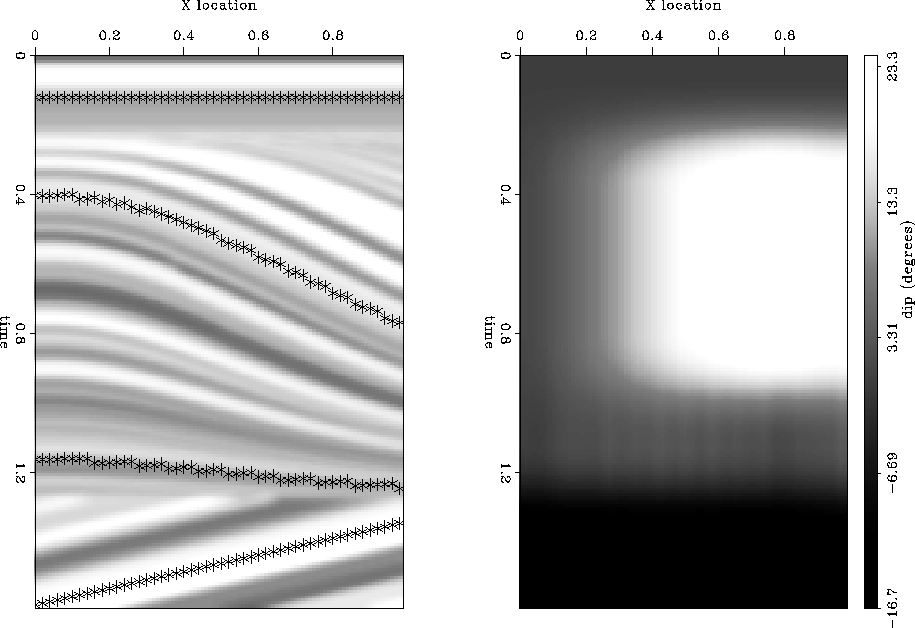
We use as our a priori information source, reflector dips,
to build our steering filters, and thus our operator ![]() .
For this test we pick our dips from our ``goal'',
left portion of Figure 5.
We define areas in which we believe each of these dips to be
approximately correct, and smooth the overall
field (right portion of Figure 5).
.
For this test we pick our dips from our ``goal'',
left portion of Figure 5.
We define areas in which we believe each of these dips to be
approximately correct, and smooth the overall
field (right portion of Figure 5).
 |
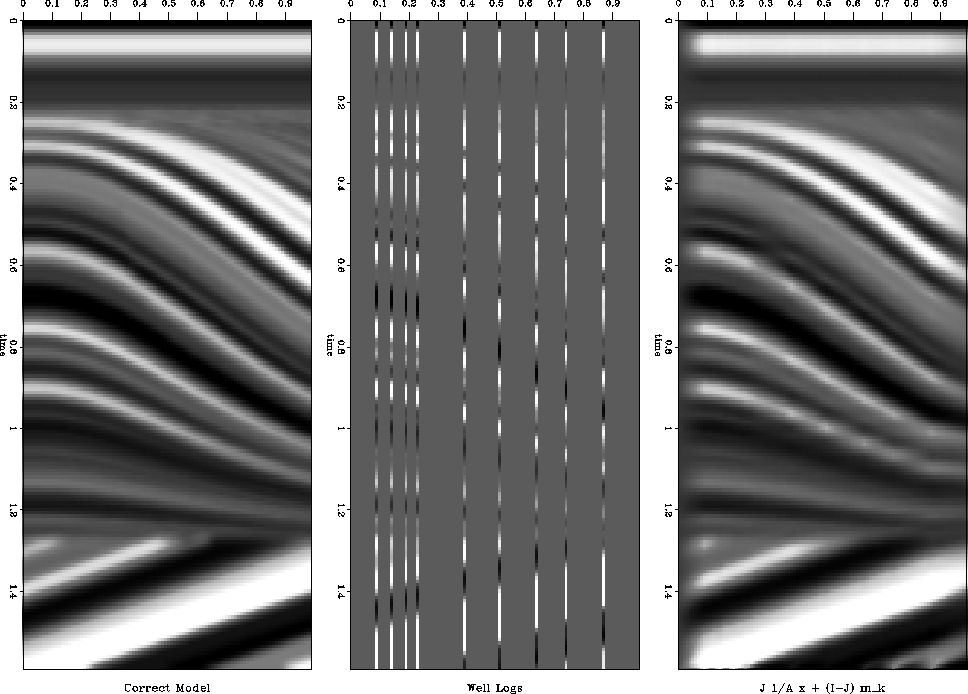
For the first test, we simulate nine well logs along the survey
(Figure 6). We use equation (18) as our
fitting goal and a conjugate gradient solver to estimate ![]() .Within 12 iterations we have a satisfactory
solution(Figure 6).
If you look closely, especially near the bottom of the section you
can still see the well locations, but in general the solution
converges quickly to something
fairly close to the correct velocity field (Figure 5).
.Within 12 iterations we have a satisfactory
solution(Figure 6).
If you look closely, especially near the bottom of the section you
can still see the well locations, but in general the solution
converges quickly to something
fairly close to the correct velocity field (Figure 5).
 |
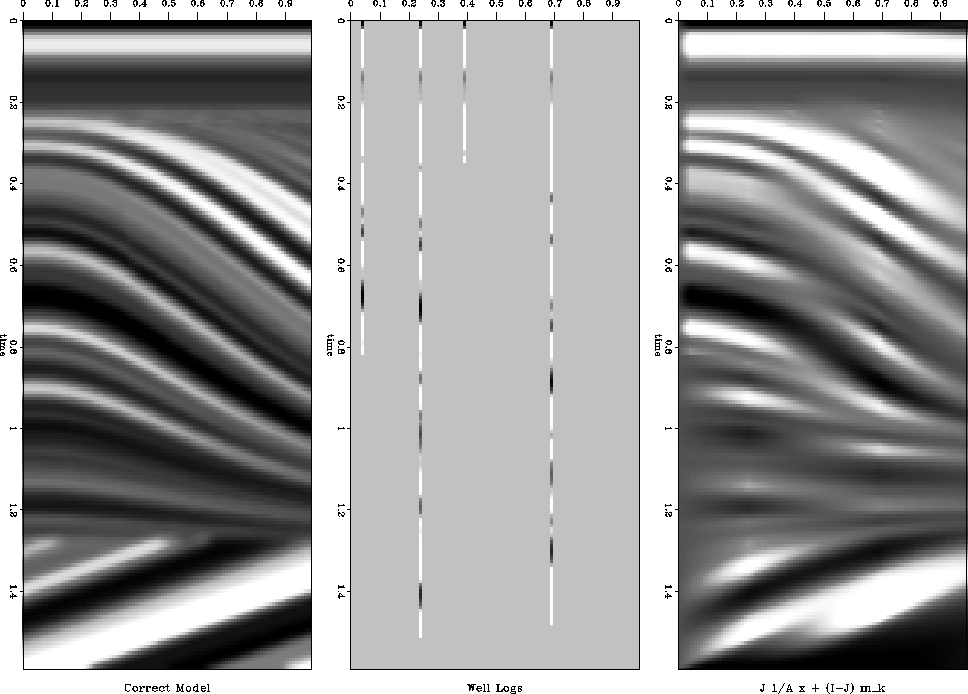
For a more difficult test, we decreased the number of wells, and give them varying lengths. In Figure 7 you see that in a few iterations we achieve a result quite similar to our goal. In addition, in areas far away from known data the method still followed the general dip direction simply at a lower frequency level.
 |