Simple algebraic rationalization of (2) yields
| |
(21) |
| |
(22) |
As described by Bancroft et al. 1995, EOM is a PSI type process
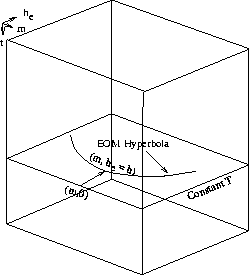
explained geometrically by Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The solid line in
this figure represents the hyperbolic equivalent offset curve
associated with the point (m,h,T) in the constant time-slice
defined by T. The amplitude at time T on a trace with midpoint m and offset h
is mapped to every point on this solid curve.
Note that EOM is a diffraction-stack process so that each input point at constant time T
and fixed offset h corresponds to a hyperbolic trajectory
indexed by T with the new offset, he, varying as a function of equation (22).
Computationally, the algorithm will have characteristics
similar to those of standard prestack-Kirchhoff approaches. One can reduce the number
of calculations by carefully limiting offset sampling, but the net result is an
algorithm whose order is still proportional to n3.
That is, the number of calculations required to move input
data is directly proportional to the number of points in the
output volume, and so is of order n3 for two-dimensional problems.
. The solid line in
this figure represents the hyperbolic equivalent offset curve
associated with the point (m,h,T) in the constant time-slice
defined by T. The amplitude at time T on a trace with midpoint m and offset h
is mapped to every point on this solid curve.
Note that EOM is a diffraction-stack process so that each input point at constant time T
and fixed offset h corresponds to a hyperbolic trajectory
indexed by T with the new offset, he, varying as a function of equation (22).
Computationally, the algorithm will have characteristics
similar to those of standard prestack-Kirchhoff approaches. One can reduce the number
of calculations by carefully limiting offset sampling, but the net result is an
algorithm whose order is still proportional to n3.
That is, the number of calculations required to move input
data is directly proportional to the number of points in the
output volume, and so is of order n3 for two-dimensional problems.
The presence of v2T2 in the denominator of (22) shows that EOM cannot proceed without knowledge or reasonable estimates of the velocity v. Clearly, the accuracy with which v is known has a direct and immediate bearing on the accuracy of the final migration. With the exception of the fact that residual NMO can improve the final image, one can expect the result of EOM to be basically similar to a good quality standard Kirchhoff migration.
 |
To fully understand the similarities between EOM and DMO-PSI, one can attempt to follow the logic of equations (16), (18), (19), and (20). Repeating the exercise with (21) replacing (13) and m0 = me yields
| |
(23) |
| |
(24) |
| |
(25) |
At first glance, the similarity of (25) with respect to (18) gives hope that EOM can be accomplished in the same manner as PSI. This is indeed true in theory. Equation (25) can be solved for (m - me) via the standard formula for finding the roots of quadratic polynomials. Ignoring the obvious root-selection analysis that will have to be made, the resulting me can be substituted into (22) to specify he in terms of m and h. The two equations in me, and he could in theory be used in the same manner as (19) and (20). Unfortunately, no simple process for performing the indicated operations presents itself. One is still forced to use a diffraction stack methodology.
In the limit, as v2T2 approaches infinity, (25) becomes (18). Thus, EOM is asymptotically equivalent to PSI. Although beyond the scope of this paper, one is lead to consider the similarity between EOM and PSI in the absence of DMO and when each is followed by residual NMO. One might expect that for large v2T2, differences will be minor. In this case, errors in v will also be inconsequential, so the claim Bancroft (1997) of weak dependence on v is probably valid. On the other hand, the asymptotic equvalence of EOM and PSI suggest that when v2T2 is small, DMO-PSI will have an image-quality advantage.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) summarize the basic similarities between EOM and PSI.
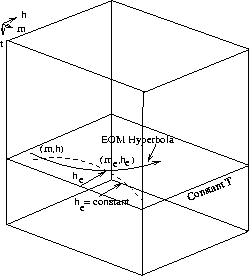
The solid curves in these figures are the equivalent-offset hyperbola and the PSI circle.
The dotted curve in Figure
summarize the basic similarities between EOM and PSI.
The solid curves in these figures are the equivalent-offset hyperbola and the PSI circle.
The dotted curve in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) schematically represents the locus of points (m,h,T) which map to (me,he,T), and is the
equivalent of PSI's dotted circle in Figure
schematically represents the locus of points (m,h,T) which map to (me,he,T), and is the
equivalent of PSI's dotted circle in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
That is, the required amplitudes at (me,he) or (m0,h0)
can be obtained either by diffracting along the
solid curves or by summing over
the dotted curves. In the limit, Figure
.
That is, the required amplitudes at (me,he) or (m0,h0)
can be obtained either by diffracting along the
solid curves or by summing over
the dotted curves. In the limit, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) will become exactly equivalent to
Figure
will become exactly equivalent to
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Conceptually, these processes are almost identical.
. Conceptually, these processes are almost identical.
Since it is not obvious how to formulate EOM as (f,k) modeling, it is
not clear that it can be implemented as an ![]() algorithm.
The net impact is that the current best formulation of EOM on
constant time slices is computationally equivalent to standard Kirchhoff migration
techniques.
algorithm.
The net impact is that the current best formulation of EOM on
constant time slices is computationally equivalent to standard Kirchhoff migration
techniques.
 |