




Next: From kinematics to dynamics
Up: Alkhalifah and Fomel: Anisotropy
Previous: Linearization
According to the classic rules of mathematical physics, the
solution of the kinematic equations (15) and (16)
can be obtained by solving the following system of ordinary
differential equations:
|  |
|
| (20) |
Here m stands for either v or  ,
,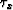 =
=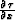 ,
,  . To trace the v and
. To trace the v and  rays, we must first
identify the initial values x0,
rays, we must first
identify the initial values x0,  ,
,  , and
, and
 from the boundary conditions. The variables x0 and
from the boundary conditions. The variables x0 and
 describe the initial position of a reflector in a
time-migrated section,
describe the initial position of a reflector in a
time-migrated section,  describes its migrated slope, and
describes its migrated slope, and
 is simply
is simply  .
.
Using the exact kinematic expressions for f results in rather
complicated representations of the ordinary differential equations.
The linearized expressions, on the other hand, are simple and allow
for a straightforward analytical solution.





Next: From kinematics to dynamics
Up: Alkhalifah and Fomel: Anisotropy
Previous: Linearization
Stanford Exploration Project
11/11/1997

