Prestack phase-shift migration

To perform the phase-shift migration in the prestack domain, the zero-offset dispersion relation must be replaced by the double-square-root (DSR) equation. An additional Fourier transform over offset is also needed.

Constant velocity prestack migration, with output provided in two-way vertical time, in offset-midpoint coordinates (Yilmaz, 1979) in given by:  

$$g(t=0,k_x,h=0,\tau)= {\int d\omega \int d k_h \; e^{i\omega \tilde{p}_{\tau}(p_x,p_h)\tau} F(\omega,k_x,k_h,\tau=0)},$$ (10)

where $F(\omega,k_x,k_h,\tau=0)$ is the 3-D Fourier transform of the field $f(t,y,h,\tau=0)$ recorded at the surface using:

$$F(\omega,k_x,k_h,\tau=0)= \int dt \; e^{-i\omega t} \int dy e^{i\omega k_xx} \int dh e^{i\omega k_hh} f(t,x,h,\tau=0),$$

and $k_x= 2 \omega p_x$, $k_h= 2 \omega p_h$, and $k_z= 2 \frac{\omega}{v} p_{\tau}$.In this paper, I will freely alternate between the half offset, h, and the full offset, X, in representing the offset axis, where X=2h. The phase factor $\tilde{p}_{\tau}(p_x,p_h)$, for isotropic media, is defined in the dispersion relation as  

$${\tilde{p}_{\tau}(p_x,p_h)} \equiv { \frac{1}{2} (\left[1 - ... ...{1 \over 2} +\left[1 - v^2 (p_x-p_h)^2\right]^{1 \over 2}) },$$ (11)

which is a normalized version of the double-square-root (DSR) equation. The two integrals in $\omega$ and k_h in equation (10) represent the imaging condition for zero-offset and zero time (h=0,t=0).

Equation (10) with the proper values of p_h and p_x to avoid imaginary values of $\tilde{p}_{\tau}$ (Popovici, 1993) can be used to do prestack migration. To obtain real values of $p_{\tau}$ that satisfy the downward continuation ordinary differential equation  

$${{\partial^2 W} \over {\partial \tau^2}}= -\omega^2 \tilde{p}_{\tau}^2 W,$$ (12)

p_x and p_h must satisfy:

$$\left \{ \begin{array} {lcl} {1 \over v} & \geq & \mid p_x+p... ... \\ {1 \over v} & \geq & \mid p_x-p_h \mid .\end{array}\right .$$

Both conditions are satisfied by insuring that  

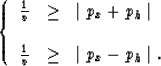
$$\begin{array} {lcl} \mid p_x \mid + \mid p_h \mid & \leq & {1 \over v}.\end{array}$$ (13)

The DSR migration can be put in a form to allow for separate migration of each constant-offset section (Popovici, 1993). For migration of a separate offset section, $F(\omega,k_x,h_0,\tau=0)$, equation (10) becomes  

$$g(t=0,k_x,h=0,\tau)= {\int d\omega \int d k_h \; e^{i\omega ... ...{p}_{\tau}(p_x,p_h)\tau+ 2 p_h h_0]} F(\omega,k_x,h_0,\tau=0)},$$ (14)

where h₀ is the half-offset of that section.

The k_h integral can be evaluated using the stationary phase method. As shown in Appendix A, the stationary point for isotropic homogeneous media is obtained by finding the maximum (with respect to p_h) of the following equation:  

$$T(p_h)= 0.5 \tau \left[ \; \sqrt{1.0 - (p_x+p_h)^2} v^2 + \sqrt{1.0 - (p_x-p_h)^2} v^2 \; \right] + 2 p_h h.$$ (15)

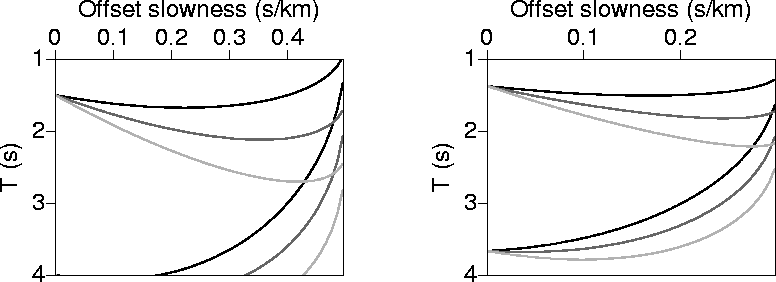
Figure 1 shows T, with $p_{\tau}$ given by equation (17), as a function of p_h for p_x=0 (a horizontal reflector) and for p_x=0.2 (a dipping reflector). To insure that $p_{\tau}$ remains real, p_h in Figure 1 ranges between 0 and ${1 \over v}-p_x$. Clearly, T in Figure 1 is multivalued; The first branch, corresponding to lower T values, represents the case in which rays from both the source and receiver have angles less than 90 degrees with the vertical (at the reflection point). The second branch corresponds to rays from either the source or receiver being overturned at the reflection point. Although the second branch is not applicable to homogeneous media (rays have always a 90-degree or less angle with the vertical), it has important implications for overturned rays in v(z) media. For large offsets and steep reflectors in a v(z) medium, the maximum of T (stationary point solution) usually exists in the second branch (higher T values).

Notice the relatively small curvature that T experiences near its maximum (the solution of the stationary phase problem). The curvature is even smaller for the dipping reflector example. This is a key to obtaining good analytical approximations in solving for p_h. The insensitivity of T to p_h around the solution implies that even an imperfect p_h can result in a good estimate of T. When all is said and done, it is the accuracy of T, which describes the phase shift, that matters the most.

 

tploteta0
Figure 1 Left: the phase factor, T, as a function p_h for a horizontal reflector (p_x=0). Right: T as a function p_h for a dipping reflector (p_x=0.2). The medium is isotropic and homogeneous with v=2 km/s. The black curve corresponds to an offset-to-vertical-time ratio ($\frac{X}{\tau}$) of 1.0 km/s, the dark-gray curve corresponds to $\frac{X}{\tau}$=2.0 km/s, and the light gray curve corresponds to $\frac{X}{\tau}$=3.0 km/s.

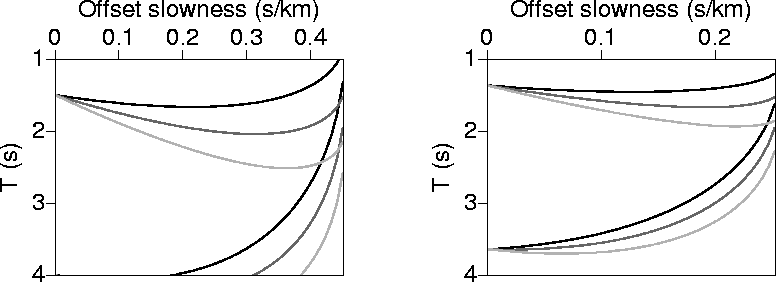
For VTI media, T is slightly more complicated than its isotropic counterpart, and is given by  

$$T(p_h) = 0.5 \tau \left[\sqrt{1-\frac{(p_x+p_h)^2 v^2}{1-2 \... ...c{(p_x-p_h)^2 v^2}{1-2 \eta v^2 (p_x-p_h)^2}} \right] + 2 p_h h$$ (16)

Appendix B. Figure 2 shows T for a VTI medium with v=2 km/s and $\eta$=0.2, again for a horizontal reflector (p_x=0) and a dipping one (p_x=0.2). Now, p_h ranges between 0 and ${1 \over {v \sqrt{1+2\eta}}}-p_x$, because $p v \sqrt{1+2\eta}$, where p is the ray parameter and must be smaller or equal 1 to avoid evanescent waves. The conclusion regarding the curvature and its implications, described in the isotropic case, holds here as well.

 

tploteta2
Figure 2 Same as in Figure 1, but for a VTI medium with $\eta$=0.2.