




Next: Solution
Up: Problem formulation
Previous: Problem formulation
To obtain the solution (1), let us assume the
existence of a function basic 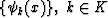 , such
that the function f (x) can be represented by a linear combination
of the basis functions, as follows:
, such
that the function f (x) can be represented by a linear combination
of the basis functions, as follows:
|  |
(7) |
The linear coefficients ck can be found by multiplying both
sides of equation (7) by one of the basis functions
(e.g. 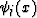 ). Inverting the equality
). Inverting the equality
| 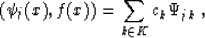 |
(8) |
where the parentheses denote the dot product, and
| 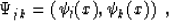 |
(9) |
gives us the following explicit expression for the coefficients
ck:
| 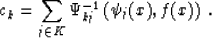 |
(10) |
Here 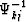 refers to the kj component of the matrix,
inverse to
refers to the kj component of the matrix,
inverse to 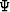 . The matrix
. The matrix 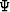 is invertible as long as the
basis set of functions is linearly independent. In the special case of
an orthonormal basis,
is invertible as long as the
basis set of functions is linearly independent. In the special case of
an orthonormal basis, 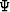 reduces to the identity matrix:
reduces to the identity matrix:
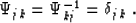
Equation (10) is a least-square estimate of the coefficients
ck. For a given set of basis functions, it approximates the
function f in formula (1) in the least-square sense.





Next: Solution
Up: Problem formulation
Previous: Problem formulation
Stanford Exploration Project
11/11/1997
![]()