




Next: HOW MUCH DAMPING?
Up: Claerbout: Preconditioning and scalingPreconditioning
Previous: ROW NORMALIZATION, NON-POSITIVE OPERATORS
I remind you of the ``standard trick''
used by Bill Symes, Bill Harlan, and probably many others.
In geophysical fitting we generally have two goals,
the first being data ``fitting''
and the second being the ``damping'' or ``regularization'' goal.
| 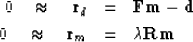 |
(1) |
| (2) |
where 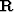 is a roughening operator.
Since the roughening operator
is a roughening operator.
Since the roughening operator 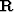 is somewhat arbitrarily chosen,
presumably we can know an inverse to it,
a smoothing operator
is somewhat arbitrarily chosen,
presumably we can know an inverse to it,
a smoothing operator 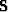 so that
so that 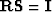 .In the simple one-dimensional case, the roughener
is a first or second derivative operator
and the smoother is a single or double integral.
(I'm not so sure that the multidimensional case
is as easy as we often like to pretend).
We define a new variable
.In the simple one-dimensional case, the roughener
is a first or second derivative operator
and the smoother is a single or double integral.
(I'm not so sure that the multidimensional case
is as easy as we often like to pretend).
We define a new variable
 by
by
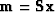 and have a set of regression goals
for which iterative methods generally converge faster:
and have a set of regression goals
for which iterative methods generally converge faster:
| 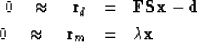 |
(3) |
| (4) |
After solving for  we easily find
we easily find 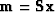 .
.
A problem arises when we do not start from 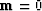 .Then before we can get started we need to find
.Then before we can get started we need to find 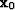 by solving
by solving 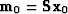 .
.





Next: HOW MUCH DAMPING?
Up: Claerbout: Preconditioning and scalingPreconditioning
Previous: ROW NORMALIZATION, NON-POSITIVE OPERATORS
Stanford Exploration Project
11/11/1997
![]() .Then before we can get started we need to find
.Then before we can get started we need to find ![]() by solving
by solving ![]() .
.