




Next: COMMON-AZIMUTH IMAGING OF A
Up: Biondi: Common-Azimuth Imaging
Previous: AZIMUTH-MOVEOUT TRANSFORMATION
Common-azimuth migration is the second component of the
common-azimuth imaging procedure.
Common-azimuth migration Biondi and Palacharla (1996) is based on a downward-continuation
operator derived from the full 3-D prestack downward-continuation
operator.
Common-azimuth data sets are recursively evaluated
at increasing depth levels,
starting from the common-azimuth data set
recorded at the surface.
Common-azimuth data has zero cross-line offset, and thus it is only four-dimensional.
Consequently, the common-azimuth
operator is also only four dimensional,
whereas the full 3-D prestack downward continuation
operator is five dimensional.
This reduction in dimensionality of the continuation
operator results in a substantial reduction
of computational and storage requirements,
though at the cost of some potential loss in accuracy.
The full prestack downward continuation operator
is expressed in the frequency-wavenumber domain
by the Double Square Root (DSR) dispersion relation
| ![\begin{eqnarray}
k_z& = &
\sqrt{
\frac{\omega^2}{v({{\bf \vec s},z)}^2} -
\fra...
..._{{x}}+k_{hx}\right)^2 + \left(k_{{y}}+k_{hy}\right)^2 \right]}
,\end{eqnarray}](img20.gif) |
|
| (2) |
where 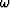 is the temporal frequency, kx and ky are the
midpoint wavenumbers, and khx and khy are the offset wavenumbers;
is the temporal frequency, kx and ky are the
midpoint wavenumbers, and khx and khy are the offset wavenumbers;
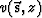 and
and 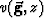 are respectively the propagation
velocities at the source and receiver location.
are respectively the propagation
velocities at the source and receiver location.
A stationary-phase approximation of the full DSR
yields the common-azimuth dispersion relation.
This new dispersion relation can be expressed as
the cascade of two 2-D relations.
The first relation is that for 2-D prestack downward-continuation
along the in-line direction,
| ![\begin{displaymath}
k_{z_{x}}=
\sqrt{
\frac{\omega^2}{v({{\bf \vec s},z)}^2} - ...
...2} -
\frac{1}{4}
\left[\left(k_{x_m}+k_{x_h}\right)^2 \right]}\end{displaymath}](img24.gif) |
(3) |
and the second relation is the one for 2-D zero-offset downward continuation
along the cross-line axis,
| 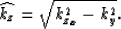 |
(4) |
The common-azimuth downward continuation operator
is not as a general operator as the full DSR,
and consequently it introduces some approximations.
However, the components of the wavefield that contribute
significantly to the final image are correctly
extrapolated Biondi and Palacharla (1996).





Next: COMMON-AZIMUTH IMAGING OF A
Up: Biondi: Common-Azimuth Imaging
Previous: AZIMUTH-MOVEOUT TRANSFORMATION
Stanford Exploration Project
11/11/1997
![\begin{eqnarray}
k_z& = &
\sqrt{
\frac{\omega^2}{v({{\bf \vec s},z)}^2} -
\fra...
..._{{x}}+k_{hx}\right)^2 + \left(k_{{y}}+k_{hy}\right)^2 \right]}
,\end{eqnarray}](img20.gif)
![\begin{eqnarray}
k_z& = &
\sqrt{
\frac{\omega^2}{v({{\bf \vec s},z)}^2} -
\fra...
..._{{x}}+k_{hx}\right)^2 + \left(k_{{y}}+k_{hy}\right)^2 \right]}
,\end{eqnarray}](img20.gif)