




Next: Estimating the prediction filter
Up: REFERENCES
Previous: REFERENCES
Here, we extend prediction filter theory to N plane waves. Assume that the
data have N plane waves with different dipping angles, the dataset can then be
expressed by
| 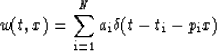 |
(22) |
Fourier transform along the time axis will give us
| 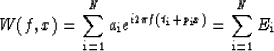 |
(23) |
where 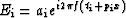 .
.
Trace 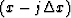 is represented by
is represented by
| 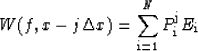 |
(24) |
where propagator 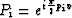 .Assuming trace
.Assuming trace 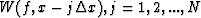 is known, trace W(f,x) can
be predicted by a N points prediction filter
is known, trace W(f,x) can
be predicted by a N points prediction filter
| 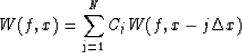 |
(25) |
Inserting equation (23) into equation (25)
| 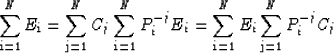 |
(26) |
For each 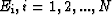
| 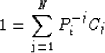 |
(27) |
Equation (27) can be expressed in matrix form
| ![\begin{displaymath}
\left[\begin{array}
{c}
1 \\ 1 \\ . \\ 1 \end{array} \ri...
...array}
{c}
C_1 \\ C_2 \\ . \\ C_{\rm N} \end{array} \right]\end{displaymath}](img61.gif) |
(28) |
Equation (28) is a Van der Monde system. This system guarantees that
there is one solution. So every 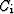 is a function of
is a function of 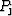 .
This means that the prediction filter relies on frequency in the case of
frequency-independent grid; whereas in the case of frequency-dependent
grids, we can still get a prediction filter which is independent from
frequency.
.
This means that the prediction filter relies on frequency in the case of
frequency-independent grid; whereas in the case of frequency-dependent
grids, we can still get a prediction filter which is independent from
frequency.





Next: Estimating the prediction filter
Up: REFERENCES
Previous: REFERENCES
Stanford Exploration Project
11/11/1997
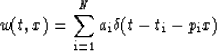
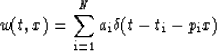
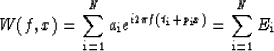
![]() is represented by
is represented by
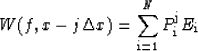
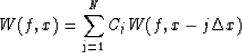
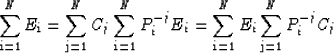
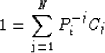
![\begin{displaymath}
\left[\begin{array}
{c}
1 \\ 1 \\ . \\ 1 \end{array} \ri...
...array}
{c}
C_1 \\ C_2 \\ . \\ C_{\rm N} \end{array} \right]\end{displaymath}](img61.gif)