Solving a block linear problem using IGF90 objects and operators

In this example, we solve the 2-D inverse linear interpolation problem: given some data values sprinkled on the (x,y) plane, we need to find a function on a uniform mesh from which we can extract the data by linear interpolation. The solution is constrained to minimize the power of a given filter applied to it. The regression  

$$\left[\begin{array} {c} {\bf d} \\ {\bf 0} \end{array} \r... ...in{array} {c} {\bf L} \\ {\bf C} \end{array} \right] {\bf x}$$ (1)

expresses the problem at hand. $\bf d$ is the data we want to extract by linear interpolation $\bf L$ from a model $\bf x$, constrained so that the application of a filter with an operator $\bf C$ has minimum power.

The following lines of code show the creation and invocation of a conjugate gradient solver CGstep solver, which iterates the regression expressed in equation (1):

  #include "CGstepSolver.h"
  ...

  // Create the CG solver
  float tol;  if(!fetch("Tol","f",&tol))  tol = 1.0e-2;
  int niter; if(!fetch("niter","d",&niter))  niter = 50;

  CGstep * solver = new CGstep( tol, niter );

  // set debug parameter for solver
  solver->Parameters().PutValue("Trace", 1);

  // Run the CG solver
  solver->Solve( N , lhs, x );

  // Output result
  x.Write();

The code consists of three concise steps: first, the block operator N, the input x and the output lhs are constructed (not shown); secondly, the solver is constructed; finally, the input data is inverted using the solver. The syntax solver->Parameters() .PutValue("Trace", 1) sets a flag for the solver to output the convergence rate to stdout. Figure 4 displays the result obtained after 70 iterations using a Laplacian filter.

The CGstep class is derived from the HCL_LinearSolver abstract base class. The HCL_LinearSolver class has only one member function, Solve(). This function takes as its arguments a linear operator, a vector that is the left hand side of the regression in equation (1), and a vector that is the solution to the regression. The CGstep class implements the Solve() member function as a conjugate gradient algorithm.

 

cgslvbkop Figure 4 Solution obtained to the seabeam missing data problem after 70 iterations, using a Laplacian filter.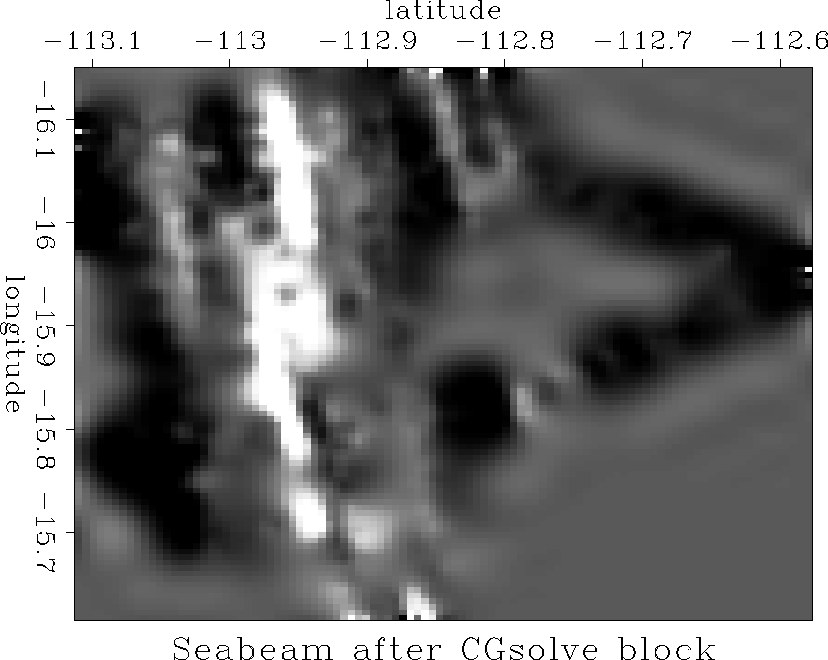