 |
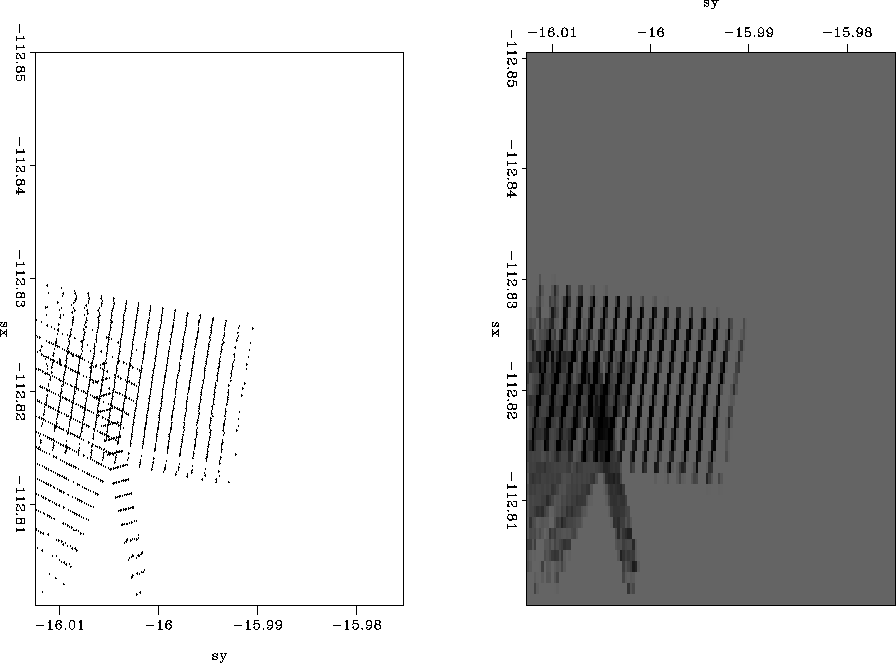
Figure 2 Left plot shows input sample locations, right plot shows the result of using the interpolation operator.
module linear_interp2d_mod use sep_f90_lib_mod !allows access to sepf90 library use sep_adjnull_mod !sep90 style adjnull !useful hold values real,save,private,pointer,dimension(:) :: dat_vec real,save,private,pointer,dimension(:,:) :: mod_vec real,save,private,pointer,dimension(:) :: f1,f2,g1,g2 integer,save,private,pointer,dimension(:) :: ix,iy integer :: ntr contains
To set up the operator we need to do some initialization, related to the
C++ concept of instances.
subroutine interp2dinitn(model,data,key1_in,key2_in){
character(len=*),intent(in)::key1_in,key2_in
type(sep_90),pointer ::data,model
real,pointer,dimension(:) :: sx,sy
integer,save,private :: n2,n3
real,save,private :: o2,d2,o3,d3
real ::tempr
integer temp_int
!Try to find keys
key1=find_key(model%keys,key1_in);key2=find_key(model%keys,key2_in)
o2=model%o(2);d2=model%d(2) ;n2=model%n(2) !set up some useful variables
o3=model%o(3); d3=model%d(3);n3=model%n(3) !for operator
ntr=size(data%traces)
nullify(mod_vec,dat_vec,sx,sy) !nullify pointer arrays
!Get sx and sy values
call get_key_values(data,key1,sx); call get_key_values(data,key2,sy)
!allocate arrays that describe irregular data's position on regular grid
allocate(f1(ntr),f2(ntr),g2(ntr),g1(ntr),ix(ntr),iy(ntr))
#set up
do i2=1,ntr{
tempr=sx(i2) - o2 /d2;temp_int=floor(tempr);ix(i2)= 1+temp_int
if(ix(i2) > 0 && ix(i2) < n2) {
f1(i2)= tempr-temp_int
tempr=sy(i2) - o3)/d3 ;temp_int=floor(tempr) ;iy(i2)= 1+temp_int
if(iy(i2) > 0 && iy(i2) < n3) f2(i2)= tempr-temp_int;g2(i2)=1.- f2(i2)
else f2(i2)=0. }
else f1(i2)=0.0
}
g1=1.-f1; g2=1.-f2
deallocate(sx,sy)
}
Finally there is the operator that actually performs the
linear interpolation.
subroutine linear_interp2d(adj,model,data){ !their is no concept of add in
!goon
logical,intent(in) :: adj
type(sep_90),pointer :: model,data
integer :: i2
call sep_adjnull(adj,model,data) !call a sep90 version of adjnull
!transfer from a sep90 dataset into regular arrays
call get_trace_slice(model,mod_vec);call get_trace_vector(data,dat_vec)
do i2=1,ntr{
if(.not. adj )
dat_vec(i2)=dat_vec(i2) + g2(i2) *g1(i2) *mod_vec(ix(i2),iy(i2)) +
f1(i2) * g2(i2) * mod_vec(ix(i2)+1,iy(i2)) + g2(i2) * f2(i2) *
mod_vec(ix(i2),iy(i2)+1) + f1(i2) * f2(i2) * mod_vec(ix(i2)+1,iy(i2)+1)
else{
mod_vec(ix(i2),iy(i2))=mod_vec(ix(i2),iy(i2)) +
dat_vec(i2) * g2(i2) *g1(i2)
mod_vec(ix(i2)+1,iy(i2))=mod_vec(ix(i2)+1,iy(i2)) +
dat_vec(i2) * g2(i2) *f1(i2)
mod_vec(ix(i2),iy(i2)+1)=mod_vec(ix(i2),iy(i2)+1) +
dat_vec(i2) * f2(i2) *g1(i2)
mod_vec(ix(i2)+1,iy(i2)+1)=mod_vec(ix(i2)+1,iy(i2)+1) +
dat_vec(i2) * f2(i2) *f1(i2)
}
}
!Put data back into septype
call put_trace_slice(model,mod_vec);call put_trace_vector(data,dat_vec)
}
 |
The program interp.r90 executes a single adjoint operation of the linear_interp2d operator above. Note the construction of the regular space, the initialization of the sep_90 variables, and the application of the adjoint through the standard operator interface.