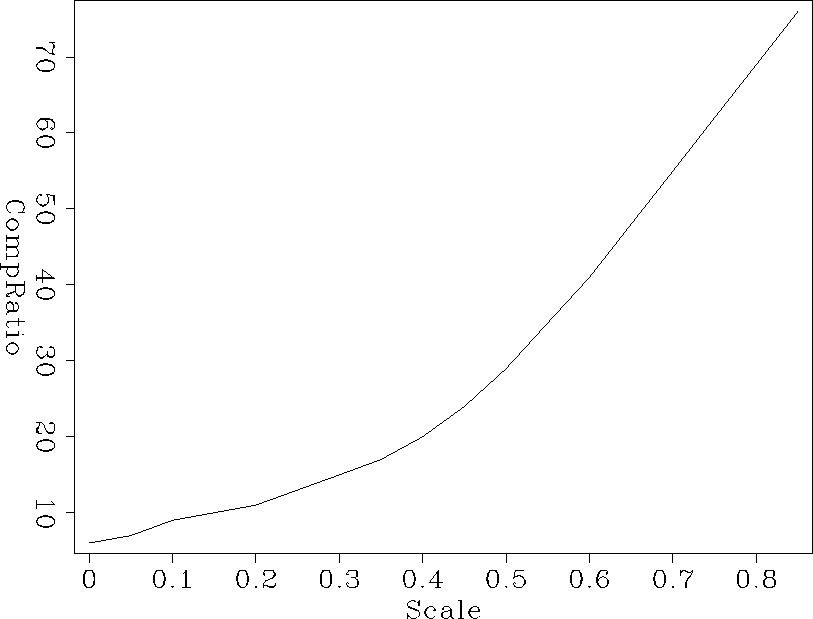Next: Synthetic 3-D data
Up: APPLICATION OF WAVELET-BASED COMPRESSION
Previous: APPLICATION OF WAVELET-BASED COMPRESSION
The synthetic shot gather consists of three hyperbolas.
The dataset has been contaminated by random noise. For this 2-D dataset,
n1=512 and n2=128. Figure 3,
4, 5, and 6 are the
t-x domain and f-k domain results.
compcsg
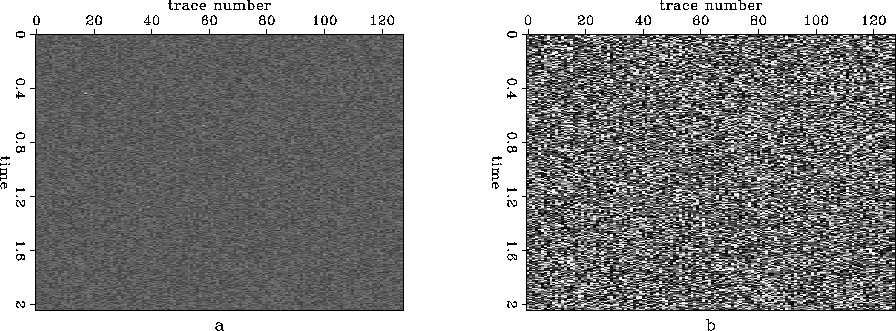
Figure 3 Synthetic shot gather in the
t-x domain (scale = 0.715). In this case, the compression ratio is 50 and SNR is 7.69dB. The two figures are plotted on the same scale.
a: Original dataset.
b: Compressed/decompressed dataset.




 compcsgdiff
compcsgdiff
Figure 4 Difference of the two results in last figure. There is little remnant of the three hyperbolas in the figure.
a: Difference shown on the absolute scale.
b: Difference shown on the relative scale.




 ftcompcsg
ftcompcsg
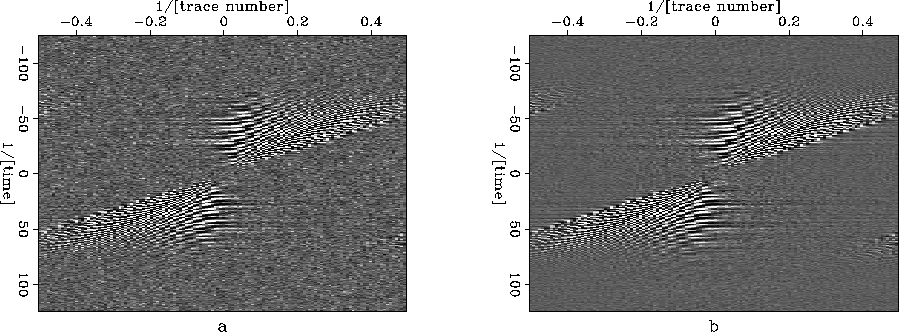
Figure 5 Synthetic shot gather in the f-k domain.
a: Original dataset.
b: Compressed/decompressed dataset.




 ftcompcsgdiff
ftcompcsgdiff
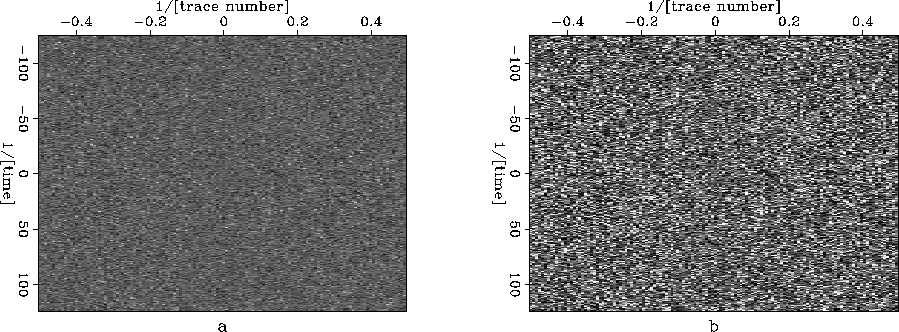
Figure 6 Difference of the two results in last figure. High frequency noise is the main component of this figure.
a: Difference shown on the absolute scale.
b: Difference shown on the relative scale.





After one compress/decompress cycle, random noise is removed from
the input dataset. It means that this technique attains high compression
ratios by filtering uncoherent component.
We conduct a series of tests using different scale
values. As shown in Figure 7 and Figure 8, with the
increase of scale value, the compression ratio increases more and more
sharply and SNR decreases more and more slowly.
csgcr
Figure 7 Compression ratio increases from 6 to 76, when scale value increases from 0.05 to 0.9.




 csgsnr
csgsnr
Figure 8 SNR decreases from 32.88dB to 7.11dB, when scale value increases from 0.05 to 0.9.










Next: Synthetic 3-D data
Up: APPLICATION OF WAVELET-BASED COMPRESSION
Previous: APPLICATION OF WAVELET-BASED COMPRESSION
Stanford Exploration Project
11/12/1997