




Next: Curved reflector in a
Up: CURVILINEAR REFLECTOR
Previous: CURVILINEAR REFLECTOR
If the reflector has the shape of a dipping plane, and the medium is
homogeneous and isotropic, the normal moveout curve is a hyperbola of
the form Levin (1971)
| 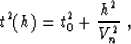 |
(60) |
where
| 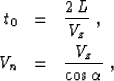 |
(61) |
| (62) |
L is the length of the zero-offset ray, and  is the
reflector dip angle. Formula (60) is not accurate if the
reflector is both dipping and curved. The Taylor series expansion of
the reflection moveout in this case has the form of equation
(26) with the coefficients Fomel (1994)
is the
reflector dip angle. Formula (60) is not accurate if the
reflector is both dipping and curved. The Taylor series expansion of
the reflection moveout in this case has the form of equation
(26) with the coefficients Fomel (1994)
| 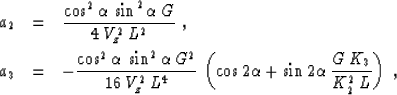 |
(63) |
| (64) |
where
| 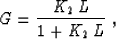 |
(65) |
 and K2 are the dip angle and curvature of the reflector at
the reflection point of the central (zero-offset) ray, and K3 is
the third-order curvature. If the reflector has an explicit
representation of the form z=z(x), then the parameters in formulas
(63) and
(64) have the expressions
and K2 are the dip angle and curvature of the reflector at
the reflection point of the central (zero-offset) ray, and K3 is
the third-order curvature. If the reflector has an explicit
representation of the form z=z(x), then the parameters in formulas
(63) and
(64) have the expressions
| 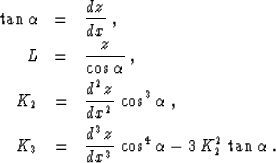 |
(66) |
| (67) |
| (68) |
| (69) |
Leaving only three terms in the Taylor series leads to the
approximation
| 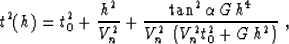 |
(70) |
where we have included the denominator in the third term to stabilize the
traveltime behavior at large offsets according to the obvious limit
| 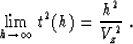 |
(71) |
As indicated by formula (68), the sign of the curvature K2 is
positive if the reflector surface is locally convex. The sign is
negative if the reflector is concave. Therefore, the coefficient G
expressed by formula (65) and, likewise, the nonhyperbolic term in
(70) can take both positive and negative values. This means
that only for concave reflectors in homogeneous media do nonhyperbolic
moveouts resemble those in VTI and vertically heterogeneous media.
Convex surfaces produce nonhyperbolic effects with the opposite sign.
For obvious reasons, formula (70) is not accurate for strong
negative curvatures 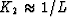 , which cause focusing of the
reflected rays and triplications of the reflection traveltimes.
, which cause focusing of the
reflected rays and triplications of the reflection traveltimes.
In order to evaluate the accuracy of approximation (70), we
can compare it with the exact expression for the case of a point
diffractor. A point diffractor is formally a convex reflector with an
infinite curvature. The exact expression for normal moveout is written
in the present notation as
| 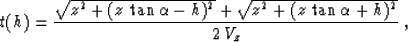 |
(72) |
where z is the depth of the diffractor, and  is the central
ray angle. Figure (
is the central
ray angle. Figure (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) shows the relative error of
approximation (70) as a function of the ray angle for the
half-offset h equal to the depth z. We can see that the maximum
error occurs at
) shows the relative error of
approximation (70) as a function of the ray angle for the
half-offset h equal to the depth z. We can see that the maximum
error occurs at 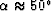 and is about 1%. We can
expect formula (70) to be even more accurate for reflectors
with smaller curvatures.
and is about 1%. We can
expect formula (70) to be even more accurate for reflectors
with smaller curvatures.
nmoerr
Figure 4 Relative error of the
nonhyperbolic moveout approximation for a curved reflector in the case
of a point diffractor. The relative error corresponds to the
half-offset h equal to the diffractor depth z and is plotted
against the central ray angle.
|
|  |










Next: Curved reflector in a
Up: CURVILINEAR REFLECTOR
Previous: CURVILINEAR REFLECTOR
Stanford Exploration Project
11/12/1997
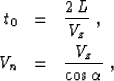
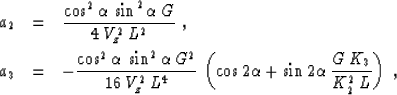
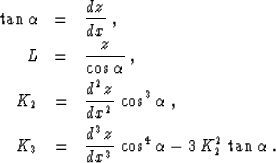
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) shows the relative error of
approximation (70) as a function of the ray angle for the
half-offset h equal to the depth z. We can see that the maximum
error occurs at
) shows the relative error of
approximation (70) as a function of the ray angle for the
half-offset h equal to the depth z. We can see that the maximum
error occurs at 