




Next: Velocity Transform
Up: EXAMPLES
Previous: Post-Stack Time Migration
In an earlier article Fomel (1994), I found the integral solution of the boundary
problem for the velocity continuation partial differential equation
Claerbout (1986)
| 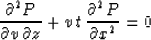 |
(73) |
with the boundary conditions 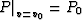 and
and
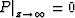 . The solution has the form
of the stacking operator (1), with the model M replaced by
P0, the summation path
. The solution has the form
of the stacking operator (1), with the model M replaced by
P0, the summation path
| 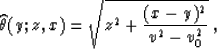 |
(74) |
the weighting function
| 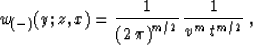 |
(75) |
which is coincident with (68), and the correction filter
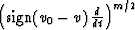 . Comparing equations
(74) and (63), we can see that this solution is equivalent
kinematically to residual migration with the velocity
. Comparing equations
(74) and (63), we can see that this solution is equivalent
kinematically to residual migration with the velocity
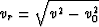 Rothman et al. (1985). The reverse operator
is the solution of equation (73) with the boundary
condition on v and has the reciprocal form of the summation path
Rothman et al. (1985). The reverse operator
is the solution of equation (73) with the boundary
condition on v and has the reciprocal form of the summation path
| 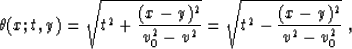 |
(76) |
the weighting function
| 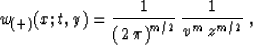 |
(77) |
and the correction filter 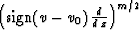 . The derivative filters are connected by the
simple asymptotic relationship
. The derivative filters are connected by the
simple asymptotic relationship
| 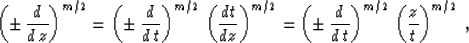 |
(78) |
which transforms the reversed velocity continuation operator to the
familiar form (31) with the weighting function equal to
(75). According to formula (69), these two operators are
seen to be asymptotically inverse.
To obtain the velocity continuation operator completely equivalent to
residual migration with the weighting function (66), we can
divide the continued wavefield by the time t, which is equivalent to
transforming equation (73) to the form
| 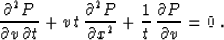 |
(79) |
The reverse continuation in this case has the weighting function
(70).
Analogously, one can obtain the pseudo-unitary residual migration with the weighting
functions (71) and (72) by dividing the
wavefield by 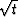 . This leads to the equation
. This leads to the equation
| 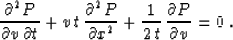 |
(80) |
It is apparent that the operators of forward and reverse continuation
with equation (73) become adjoint to each other if the
definition of the dot product is changed according to formulas
(28) and (29) with the model weight WM(z)=z
and the data weight WS(t)=t. Analogously, the solutions of equation
(79) are adjoint if 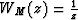 and
and 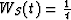 . This is a simple example of how the arbitrarily chosen definition of
the dot product can affect the basic properties of the
inverted operators.
. This is a simple example of how the arbitrarily chosen definition of
the dot product can affect the basic properties of the
inverted operators.





Next: Velocity Transform
Up: EXAMPLES
Previous: Post-Stack Time Migration
Stanford Exploration Project
11/12/1997
![]() . This leads to the equation
. This leads to the equation
![]() and
and ![]() . This is a simple example of how the arbitrarily chosen definition of
the dot product can affect the basic properties of the
inverted operators.
. This is a simple example of how the arbitrarily chosen definition of
the dot product can affect the basic properties of the
inverted operators.