Mathematical physics presents us with many partial differential equations, such as the heat-flow equation, the acoustic, seismic, or electromagnetic wave equation. Such equations are frequently simulated on computers by finite-difference approximations. In applied science we often need to find the inverse operator to such a simulation to image the source field responsible for the observed data. Many inversion methods require an implementation of the adjoint (matrix transpose) of the linear simulator process.
In this short extract of a more detailed paper (http://sepwww.stanford.edu/redoc/), we demonstrate a straightforward programming scheme to implement the adjoint to a finite-difference simulation of a linear operator.
The basic idea
is that the adjoint of a row vector
is a column vector.
So the adjoint of the equation
y=ax1+bx2
is two equations,
![]() and
and
![]() .Since we often combine operators by element-wise addition,
we often code them in the form
.Since we often combine operators by element-wise addition,
we often code them in the form
![]() .A convenient notation comes from the C computer language
where such assignments are written as
y += a*x1+b*x2.
In this case the adjoint can be implemented as
x1 += a*y and
x2 += b*y.
.A convenient notation comes from the C computer language
where such assignments are written as
y += a*x1+b*x2.
In this case the adjoint can be implemented as
x1 += a*y and
x2 += b*y.
The one-dimensional heat-flow equation can be used to represent viscosity and is the simplest place to start:
| |
(1) |
| |
(2) |
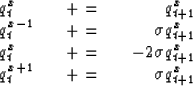 |
(3) |
A step of the heat-flow equation
transforms from qt to qt+1.
The adjoint operation (transpose matrix)
transforms qt+1 to ![]() (which in general is different
from qt),
thus stepping time backward.
Temperature smooths as time runs forward.
If we had the inverse matrix we could step backward in time
and would find the rougher temperature qt.
Running backward in time with the adjoint matrix
(which in general is different
from qt),
thus stepping time backward.
Temperature smooths as time runs forward.
If we had the inverse matrix we could step backward in time
and would find the rougher temperature qt.
Running backward in time with the adjoint matrix ![]() ,we find temperature getting smoother.
For heat-flow,
this is the main difference between
the adjoint and the inverse.
,we find temperature getting smoother.
For heat-flow,
this is the main difference between
the adjoint and the inverse.
The heat-flow operator H marches one step in time. Next, using a similar method, we should find finite-difference operators for the pressure operator P and the velocity operator V. These details are found in the electronic document referred to above. Finally, we represent the viscous scalar wave equation by the product HVP, so its adjoint is simply P'V'H'.
Any time we implement an adjoint operator, we need to confirm that we compute the correct adjoint of a forward operator. Mathematics demands that y'(Ax)=(A'y)'x for a linear operator A, its adjoint A', and ``all possible functions'' x and y. In practice, it suffices to test y'(Ax)=(A'y)'x using any set of random numbers for x and y and our program for the operators A and A'. The electronic version of this document shows that for random inputs of size 1003, the quantities y'(Ax) and (A'y)'x are equal to the expected six digits of numerical accuracy. The result of this dot-product test is stored in the file dot.txt.
Since finite-difference representations of differential equations
can be unstable,
a further necessary test of the viscous wave equation program is the
sample output below.
I put random point sources in the frog pond
on a ![]() matrix.
matrix.
![]()
FIG: A rectangular pond after a frog's random
hops disturbed its surface. The subroutines that compute
this figure are included in the electronic version of
this document.