




Next: WEIGHTED MEDIANS
Up: Claerbout: Medians in regression
Previous: MEDIANS IN AUTOREGRESSION
Our basic model is
| 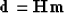 |
(9) |
where
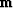 is model space,
is model space,
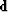 is data space, and
is data space, and
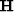 is a curve superposition such as hyperbola superposition.
Obviously we could be talking about velocity analysis or migration
and the number of components in model space is huge.
These unknown components may be partly correlated,
but since there are so many unknowns
we will suppose that it is useful
to seek an initial guess at a solution
by assuming the unknowns are not correlated.
To aid in our motivation,
we also presume the data contains much bursty noise
so the usual ways of
doing
migration
or velocity analysis
are in trouble;
thus we have a license to seek new ways that are fast and robust.
is a curve superposition such as hyperbola superposition.
Obviously we could be talking about velocity analysis or migration
and the number of components in model space is huge.
These unknown components may be partly correlated,
but since there are so many unknowns
we will suppose that it is useful
to seek an initial guess at a solution
by assuming the unknowns are not correlated.
To aid in our motivation,
we also presume the data contains much bursty noise
so the usual ways of
doing
migration
or velocity analysis
are in trouble;
thus we have a license to seek new ways that are fast and robust.
We begin by loading up a residual vector 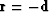 with the negative of the data.
We could start an inverse problem with a gradient, say
with the negative of the data.
We could start an inverse problem with a gradient, say
| 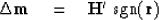 |
(10) |
but here I propose something much simpler.
We process only one component of model space.
(Later and independently we need to
process likewise all other components of model space,
and then iterate some more.)
Thus 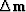 has only one nonzero component.
We may as well take that component to be unity,
say
has only one nonzero component.
We may as well take that component to be unity,
say 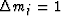 for some particular j.
This perturbation allows us to
create a perturbed residual
for some particular j.
This perturbation allows us to
create a perturbed residual 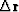 .Allow me an approximation of physics and numerical analysis
where a single point of model space does not go to every point in data space.
In the most elementary modeling procedure
the number of points in data space affected by a single point of model space
is simply the number of offsets, say nx.
The residual perturbation is
.Allow me an approximation of physics and numerical analysis
where a single point of model space does not go to every point in data space.
In the most elementary modeling procedure
the number of points in data space affected by a single point of model space
is simply the number of offsets, say nx.
The residual perturbation is
|  |
(11) |
which gives us a 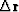 of nx affected components
and the values
of nx affected components
and the values 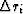 of those components are the values of
the amplitude versus offset of the hyperbola in our simple modeling.
As before,
the new model is
of those components are the values of
the amplitude versus offset of the hyperbola in our simple modeling.
As before,
the new model is
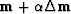 , where
, where
| 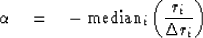 |
(12) |
It is fun to compare this iterative process to migration since it is similar,
but it leads to a kind of inversion.
To begin with, if we had no bursty noise, we could simplify
life just a little bit by choosing  to be
to be
| 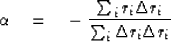 |
(13) |
This  is the usual normalization that might be used in stacking.
Since we work recursively, however,
the job
of reducing the residual is never done,
and the values on the residual plane depend
upon the order in which we do the work.
is the usual normalization that might be used in stacking.
Since we work recursively, however,
the job
of reducing the residual is never done,
and the values on the residual plane depend
upon the order in which we do the work.
We could choose to do the work in some order to
make the code fast.
We could also choose to do the work in some ``best''
order (yet to be defined) for the quality of the results.
There is no need for
the data to lie on a regular mesh
or for a ``complete'' data set.
Aliasing issues have yet to be examined.





Next: WEIGHTED MEDIANS
Up: Claerbout: Medians in regression
Previous: MEDIANS IN AUTOREGRESSION
Stanford Exploration Project
11/12/1997
![]() with the negative of the data.
We could start an inverse problem with a gradient, say
with the negative of the data.
We could start an inverse problem with a gradient, say
![]() to be
to be