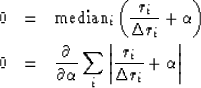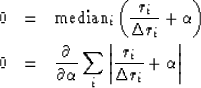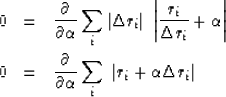Next: DISCUSSION
Up: Claerbout: Medians in regression
Previous: INVERSE HYPERBOLA SUPERPOSITION
The simple median is too simple a concept.
We need the weighted median concept
to properly allow for the fact that
a stacking hyperbola is large near its
top and tapers off with distance and angle.
A simple median is like a sum over the hyperbola
without allowing for amplitude as a function of offset.
We need to allow for amplitude with medians too.
Weighted medians are explained in FGDP,
but I give a short summary here.
These two equations are equivalent:
| 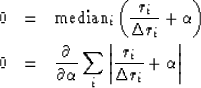 |
(14) |
| (15) |
The weighted median
with weights 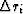 is defined instead by the
equilibrium:
is defined instead by the
equilibrium:
| 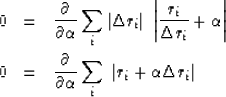 |
(16) |
| (17) |
The weighted median minimizes the so-called L1 norm of the residual
thus the weighted median seems a more standard optimization concept.
The simple median,
not the weighted median however,
is more appropriate in the autoregression problem
where noise in field data finds its way
into the operator.
(The data is in the convolution matrix (operator)
that multiplies the filter vector.)





Next: DISCUSSION
Up: Claerbout: Medians in regression
Previous: INVERSE HYPERBOLA SUPERPOSITION
Stanford Exploration Project
11/12/1997