Next: Imaging condition in plane
Up: Imaging conditions
Previous: Conventional prestack imaging
In order to retrieve the full reflectivity matrix,
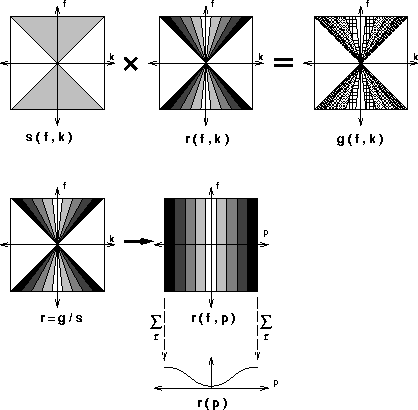
de Bruin et al. (1990) proposes another imaging condition (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Instead of deconvolving in the spatial domain,
they deconvolve in the Fourier domain
).
Instead of deconvolving in the spatial domain,
they deconvolve in the Fourier domain 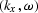 after Fourier transforming both downgoing and upcoming waves,
as follows:
after Fourier transforming both downgoing and upcoming waves,
as follows:
| 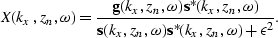 |
(52) |
The next step is to transform 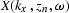 into
into  by replacing the wavenumber kx with
the ray parameter
by replacing the wavenumber kx with
the ray parameter 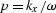 .Then imaging is carried out in the
.Then imaging is carried out in the  domain along the lines of the constant p:
domain along the lines of the constant p:
| 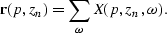 |
(53) |
This imaging condition retrieve the full angle-dependent reflectivity.
However, since the deconvolution is performed in the Fourier domain,
it implies a spatially invariant reflectivity, which is the case
of horizontal reflector in constant velocity medium.
Thus it has the disadvantage that is of being difficult to implement
a realistic model.
fk-img
Figure 5 Schematic representation of de Bruin's imaging condition






Next: Imaging condition in plane
Up: Imaging conditions
Previous: Conventional prestack imaging
Stanford Exploration Project
2/5/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Instead of deconvolving in the spatial domain,
they deconvolve in the Fourier domain
).
Instead of deconvolving in the spatial domain,
they deconvolve in the Fourier domain ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Instead of deconvolving in the spatial domain,
they deconvolve in the Fourier domain
).
Instead of deconvolving in the spatial domain,
they deconvolve in the Fourier domain ![]() after Fourier transforming both downgoing and upcoming waves,
as follows:
after Fourier transforming both downgoing and upcoming waves,
as follows: