DIP MOVEOUT

Analogous to the hyperbola push operator $\bold H$and semicircle push operator $\bold C$defined above, let us define $\bold C_h$ and $\bold H_h$for pushing ellipses and flat-topped hyperbolas. (Here h is half the shot-geophone offset.)

$$\begin{eqnarray} \vec {\bold z} &=& \bold C_h\ \vec {\bold t} \quad\quad {\rm s... ... {\rm spray\ or\ push\ a\ flattened\ hyperbola\ into\ the\ output}\end{eqnarray}$$ (9) (10)

Given data on a nonzero-offset section, we seek to convert it to a zero-offset section. Conceptually the simplest approach is to first migrate the constant offset data with an ellipsoid push operator $\bold C_h$ and then take each point on the ellipsoid and diffract it out to a zero-offset hyperbola with a push operator $\bold H_0 = \bold H_{h=0}$.The product of push operators $\bold R = \bold H_0 \bold C_h$is known as Rocca's smile. This smile operator includes both normal moveout and dip moveout. (We could say that dip moveout is defined by Rocca's smile after restoring the normal moveout.)

To visualize the Rocca smile operator more clearly, I broke the continuous ellipsoid into a sequence of dots so you would be able to see individual hyperbolas as well their superposition. This is shown in Figure 1.

 

frocca Figure 1 Rocca's smile is a superposition of hyperbolas, each with its top on an ellipse.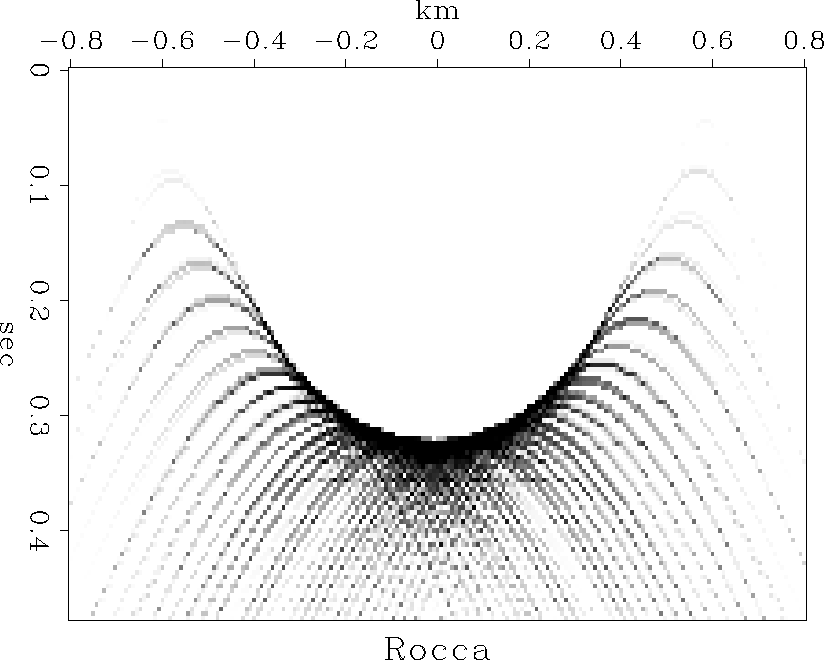

Because of the approximation $\bold H \approx \bold C'$,we have four different ways to express the Rocca smile:

$$\bold R \quad =\quad \bold H_0 \bold C_h \quad\approx\quad ... ... \bold C'_0 \bold C_h \quad\approx\quad \bold C'_0 \bold H'_h$$ (11)

$\bold H_0 \bold H'_h$ says sum over a flat-top and then spray a regular hyperbola. More interesting is the operator $\bold C'_0 \bold C_h$which says spray an ellipse and then sum over a circle. This approach, associated with Gerry Gardner, says that we are interested in all circles that are inside and tangent to an ellipse, since only the ones that are tangent will have a constructive interference. The last operator $\bold C'_0 \bold H'_h$,having two pull operators should have smoothest output. Sergey Fomel (personal communication) suggests an interesting illustration of it: Its adjoint is two push operators, $\bold R' = \bold H_h \bold C_0$.$\bold R'$ takes us from zero offset to nonzero offset first by pushing a data point to a semicircle and then by pushing points on the semicircle to flat-topped hyperbolas. As before, to make the hyperbolas more distinct, I broke the circle into dots along the circle and show the result in Figure 2.

 

sergey Figure 2 The adjoint of Rocca's smile is a superposition of flattened hyperbolas, each with its top on a circle.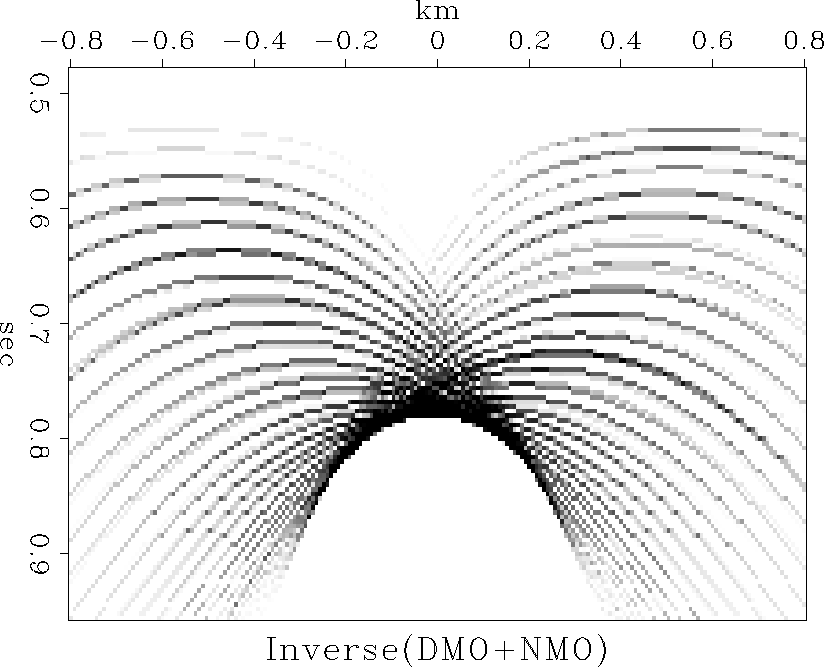

It is worth noticing that the concepts in this section are not limited to constant velocity but apply as well to v(z). The circle operator $\bold C$ presents some difficulties, however. The circle operator, a push from t to z, requires us to solve for z given t. Starting from the Dix moveout approximation, $t^2 = \tau^2 + x^2/v(\tau )^2$we can directly solve for $t(\tau ,x)$but finding $\tau (t,x)$ is an iterative process at best. At worst, when the velocity gradient is abrupt enough, $\tau (t,x)$ is multivalued. We often see this multivalued function on raw data.

# Flat topped hyperbolas and constant-offset section migration
#
subroutine flathyp(   adj, add, vel    , h, t0,dt,dx, modl,nt,nx, data)
integer ix,iz,it,ib,  adj, add,                            nt,nx
real    t, amp, z,b,            vel(nt), h, t0,dt,dx, modl(nt,nx),data(nt,nx)
call adjnull(        adj, add,                        modl,nt*nx, data,nt*nx)
do ib= -nx, nx {	b = dx * ib 		# b = midpt separation y-y0
    do iz= 2, nt {	z = t0 + dt * (iz-1)	# z = zero-offset time
	t = .5 * ( sqrt( z**2 +((b-h)*2/vel(iz))**2) +
	           sqrt( z**2 +((b+h)*2/vel(iz))**2)   )
	it = 1.5 + (t - t0) / dt
     if( it > nt )                     break
	amp = (z/t)/ sqrt(t)
	do ix= max0(1, 1-ib),  min0(nx, nx-ib)
		 if( adj == 0 )
			data(it,ix+ib)= data(it,ix+ib) + modl(iz,ix   ) * amp
		 else
			modl(iz,ix   )= modl(iz,ix   ) + data(it,ix+ib) * amp
	}
    }
return; end