




Next: The velocity operator
Up: WAVE PROCESS CHAIN
Previous: WAVE PROCESS CHAIN
The pressure operator from physics from the
``equation of state''
that the time rate of change of the pressure
is an external source s(x,y,t) minus
the divergence of the velocity times the incompressibility K.
| 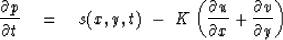 |
(11) |
In the heat flow equation the field variable
is a scalar (the temperature).
For wave propagation in two dimensions,
the wavefield variable has three components,
pressure and two components of material velocity.
The pressure operator P transforms
ptx,y to pt+1x,y
but it is an identity matrix
for the two components of velocity
(which will actually be transformed in a later process).
We distribute the wavefield variables throughout space with this tiling:
|  |
(12) |
We define the basic tile for this discrete mesh as
| 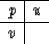 |
(13) |
Computationally we refer to this basic tile on the inputs as 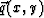 and on the outputs as
and on the outputs as 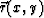 although the three components in the tile
are at slightly different physical locations
from one another.
Expressing the pressure equation for these tiles we have
although the three components in the tile
are at slightly different physical locations
from one another.
Expressing the pressure equation for these tiles we have
| ![\begin{displaymath}
p_{t+1}^x \quad =\quad s_t^x + p_t^x
- \;
{K \Delta t \ove...
...;
[
(u_t^{x,y}-u_t^{x-1,y})
+
(v_t^{x,y}-v_t^{x,y-1})
]\end{displaymath}](img31.gif) |
(14) |
In subroutine pressure() below
the input pressure and velocity field is q(x,y,*)
and the output is r(x,y,*).
Equation (14) is expressed in the subroutine
on the line beginning with
r(x,y,p)=.
# operator of pressure change from divergence of velocity
#
subroutine pressure( adj, add, kappa, q,nx,ny, r )
integer adj, add, nx,ny, x, y, p, u, v
real kappa(nx,ny),q(nx,ny,3), r(nx,ny,3)
call adjnull( adj, add, q,nx*ny*3, r,nx*ny*3)
p=1; u=2; v=3
do x= 2, nx-1 {
do y= 2, ny-1 {
if( adj == 0) {
r(x,y,p)= r(x,y,p) + q(x,y,p) - (q(x,y,u) - q(x-1,y ,u)) * kappa(x,y) -
(q(x,y,v) - q(x ,y-1,v)) * kappa(x,y)
r(x,y,u)= r(x,y,u) + q(x,y,u)
r(x,y,v)= r(x,y,v) + q(x,y,v)
} else {
q(x ,y ,p)= q(x ,y ,p) + r(x,y,p)
q(x ,y ,u)= q(x ,y ,u) - r(x,y,p) * kappa(x,y) + r(x,y,u)
q(x-1,y ,u)= q(x-1,y ,u) + r(x,y,p) * kappa(x,y)
q(x ,y ,v)= q(x ,y ,v) - r(x,y,p) * kappa(x,y) + r(x,y,v)
q(x ,y-1,v)= q(x ,y-1,v) + r(x,y,p) * kappa(x,y)
}
}}
return; end
Notice that the identity matrix ``pass through''
of the velocity components
shows up as two extra assignments in the forward operator
and thus as two added terms in the adjoint operator.
frog
Figure 1
A few frogs hopped into the pond.
Chirup!
|
|  |










Next: The velocity operator
Up: WAVE PROCESS CHAIN
Previous: WAVE PROCESS CHAIN
Stanford Exploration Project
11/12/1997

