One problem with noise removal by filtering is that the response
of the noise to the filter is left in the signal.
As an example, consider a model of the recorded data as the sum of
signal and noise, or ![]() , where
, where ![]() is the recorded data,
is the recorded data,
![]() is signal, and
is signal, and ![]() is noise.
If a signal-prediction filter
is noise.
If a signal-prediction filter ![]() is calculated from the data
is calculated from the data ![]() such that
such that
![]() ,and the noise is assumed to be what is left after the filter is applied,
,and the noise is assumed to be what is left after the filter is applied,
![]() ,is inconsistent with the original model of
,is inconsistent with the original model of ![]() .Instead the output of the filter is
.Instead the output of the filter is ![]() , since
, since ![]() ,assuming that
,assuming that ![]() .
.
An alternative to accepting this filtering result
is to set up the problem as a matrix inversion.
If the signal is predicted by a filter ![]() , such that
, such that ![]() ,the noise is predicted by a filter
,the noise is predicted by a filter ![]() , such that
, such that ![]() ,and the recorded data is a sum of the signal and noise,
,and the recorded data is a sum of the signal and noise, ![]() ,then the signal may be predicted with a system of regressions such as
,then the signal may be predicted with a system of regressions such as
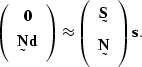 |
(1) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is solved,
) is solved,
If ![]() is difficult to estimate, or if the noise is unpredictable,
an alternative to the previous system of regressions is
is difficult to estimate, or if the noise is unpredictable,
an alternative to the previous system of regressions is
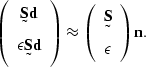 |
(2) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The calculated signal in this case is
.
The calculated signal in this case is