Next: The three-dimensional extension of
Up: Three-dimensional lateral prediction
Previous: Three-dimensional lateral prediction
Extending the t-x prediction to three dimensions is a simple matter
of defining the 3-dimensional convolution and its adjoint, that is,
its conjugate transpose.
Instead of dividing the input into 2-dimensional
windows, the input volume
is broken into 3-dimensional sub-volumes.
Each of these sub-volumes is used
in a separate least-squares problem for calculating a
3-dimensional filter, which is a straightforward extension
of the calculation of a
2-dimensional t-x filter.
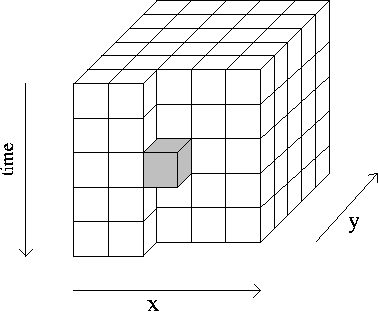
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the configuration of the 3-dimensional
filter I used.
This configuration is a modification of the more general
3-dimensional filter
shown in Claerbout 1992a, page 198.
While the 3-dimensional filter might be made symmetrical in space by
constraining the filter coefficients across the central element to be
equalGulunay et al. (1993), I simply applied the filter in multiple directions and
averaged the results.
shows the configuration of the 3-dimensional
filter I used.
This configuration is a modification of the more general
3-dimensional filter
shown in Claerbout 1992a, page 198.
While the 3-dimensional filter might be made symmetrical in space by
constraining the filter coefficients across the central element to be
equalGulunay et al. (1993), I simply applied the filter in multiple directions and
averaged the results.
DDDfilter
Figure 4
A three-dimensional lateral prediction filter.
The darkened cube is the output position.






Next: The three-dimensional extension of
Up: Three-dimensional lateral prediction
Previous: Three-dimensional lateral prediction
Stanford Exploration Project
2/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the configuration of the 3-dimensional
filter I used.
This configuration is a modification of the more general
3-dimensional filter
shown in Claerbout 1992a, page 198.
While the 3-dimensional filter might be made symmetrical in space by
constraining the filter coefficients across the central element to be
equalGulunay et al. (1993), I simply applied the filter in multiple directions and
averaged the results.
shows the configuration of the 3-dimensional
filter I used.
This configuration is a modification of the more general
3-dimensional filter
shown in Claerbout 1992a, page 198.
While the 3-dimensional filter might be made symmetrical in space by
constraining the filter coefficients across the central element to be
equalGulunay et al. (1993), I simply applied the filter in multiple directions and
averaged the results.