The problem of calculating a prediction-error filter ![]() can be set up
by describing the convolution process
as a matrix multiplication
can be set up
by describing the convolution process
as a matrix multiplication ![]() .The matrix
.The matrix ![]() is made up of shifted versions
of the signal
is made up of shifted versions
of the signal ![]() to be multiplied by the filter vector
to be multiplied by the filter vector ![]() as shown below.
If
as shown below.
If ![]() is perfectly predictable, a filter
is perfectly predictable, a filter ![]() will be calculated
to give a result of zero,
will be calculated
to give a result of zero, ![]() .
With most real data,
.
With most real data,
![]() will not be perfectly predictable,
and the result of
will not be perfectly predictable,
and the result of ![]() will not be zero, but
will not be zero, but ![]() ,where
,where ![]() is the error or unpredictable part.
This error is minimized to get the desired
is the error or unpredictable part.
This error is minimized to get the desired ![]() .The idea of an imperfect prediction
may also be expressed as a system of regressions,
where
.The idea of an imperfect prediction
may also be expressed as a system of regressions,
where ![]() .
.
Here, I will show the traditional method of setting up
a one-dimensional prediction-error filter calculation problem.
The linear system ![]() , expanded to show its elements, is
, expanded to show its elements, is
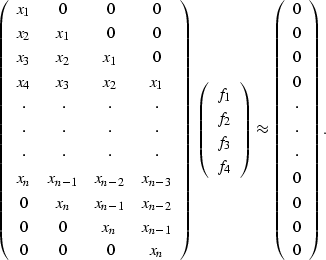 |
(41) |
Notice how the matrix ![]() is made up of the vector
is made up of the vector ![]() shifted against the filter to produce the convolution of
shifted against the filter to produce the convolution of ![]() and
and ![]() .At least one element of
.At least one element of ![]() is constrained to be non-zero to
prevent the trivial solution where all elements of
is constrained to be non-zero to
prevent the trivial solution where all elements of ![]() are zero.
In this case, f1 is constrained to be one
so we can modify the equation above to move the constrained portion to the
right-hand side to get
are zero.
In this case, f1 is constrained to be one
so we can modify the equation above to move the constrained portion to the
right-hand side to get
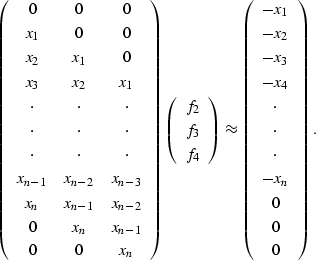 |
(42) |
![]() is the autocorrelation matrix,
which is also referred to as the inverse covariance matrix.
The reason for calling
is the autocorrelation matrix,
which is also referred to as the inverse covariance matrix.
The reason for calling ![]() an
autocorrelation matrix is obvious, since the rows of the
matrix are the shifted autocorrelation of
an
autocorrelation matrix is obvious, since the rows of the
matrix are the shifted autocorrelation of ![]() .The description of
.The description of ![]() as a covariance matrix
comes from the idea that
as a covariance matrix
comes from the idea that ![]() is a function of random variables.
The relationship between the values of
is a function of random variables.
The relationship between the values of ![]() at various lags are
described by the expectation E of the dependence of the values of
at various lags are
described by the expectation E of the dependence of the values of
![]() with different delays.
This is expressed as E(xi xj), where i and j are indices
into the series
with different delays.
This is expressed as E(xi xj), where i and j are indices
into the series ![]() .If the expectation E(xi xj) is zero when
.If the expectation E(xi xj) is zero when ![]() ,the spectrum of
,the spectrum of ![]() would be white,
and the sample values of
would be white,
and the sample values of ![]() would be unrelated to each other.
The autocorrelation would be zero except at zero lag.
would be unrelated to each other.
The autocorrelation would be zero except at zero lag.
The solution for ![]() requires storing only the autocorrelation of
requires storing only the autocorrelation of ![]() and can be solved quickly and efficiently using Levinson recursion.
Once again, the efficiency of this technique depends on
and can be solved quickly and efficiently using Levinson recursion.
Once again, the efficiency of this technique depends on
![]() being Toeplitz, which in turn depends on the type of
convolution being transient, rather than internal or truncated-transient.
When
being Toeplitz, which in turn depends on the type of
convolution being transient, rather than internal or truncated-transient.
When ![]() is not Toeplitz, it can still be solved
using techniques such as Cholesky factorization,
but at a higher cost of storage and calculation.
is not Toeplitz, it can still be solved
using techniques such as Cholesky factorization,
but at a higher cost of storage and calculation.