




Next: An example of calculating
Up: Background and definitions
Previous: Solving methods
One of the most common geophysical applications of inversion
is the calculation of prediction-error filters.
A prediction-error  is defined as
is defined as
| 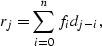 |
(26) |
where 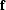 is the prediction-error filter
of length
is the prediction-error filter
of length  , and
, and  is an input data series.
The filtering operation may also be expressed as
is an input data series.
The filtering operation may also be expressed as 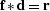 ,where
,where  indicates convolution.
For the sake of the discussion here,
indicates convolution.
For the sake of the discussion here,
 is an infinitely long time series.
As in the previous discussion,
the error
is an infinitely long time series.
As in the previous discussion,
the error  and the data
and the data  will be assumed to be
stationary and have a Gaussian distribution with a zero mean.
The error
will be assumed to be
stationary and have a Gaussian distribution with a zero mean.
The error  will also be assumed to be uncorrelated
so that
will also be assumed to be uncorrelated
so that ![$E[\sv r \sv r^{\dagger}] = \sigma_r^2 \st I$](img58.gif) .
.
Application of a prediction-error filter removes the predictable information
from a dataset, leaving the unpredictable
information, that is, the prediction error.
A typical use of prediction-error filters is seen in the deconvolution problem,
where the predictable parts of a seismic trace,
such as the source wavelet and multiples,
are removed,
leaving the unpredictable reflections.
The condition that  contains no predictable information
may be expressed in several ways.
One method is by minimizing
contains no predictable information
may be expressed in several ways.
One method is by minimizing 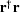 , where
, where 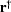 is the conjugate transpose of
is the conjugate transpose of  ,by calculating a filter that minimizes
,by calculating a filter that minimizes 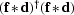 .This minimization reduces
.This minimization reduces  to have the least energy possible,
where the smallest
to have the least energy possible,
where the smallest  is assumed to
contain only unpredictable information.
is assumed to
contain only unpredictable information.
Another equivalent expression of unpredictability is that
the non-zero
lags of the normalized autocorrelation are zero,
or that
| 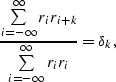 |
(27) |
where 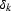 is one when k is zero and is zero otherwise.
This approximation
may also be expressed as
is one when k is zero and is zero otherwise.
This approximation
may also be expressed as ![$E[r_{i} r_{i+k}]=\sigma_r^2 \delta(k)$](img109.gif) ,where
,where 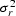 is a scale factor that may be ignored.
These two methods of expressing unpredictability
are the basis for the sample calculations
of the prediction-error presented in the next section.
is a scale factor that may be ignored.
These two methods of expressing unpredictability
are the basis for the sample calculations
of the prediction-error presented in the next section.
The prediction-error filter may also be defined
in the frequency domain using the condition that
the expectation E[ri rj] = 0 for 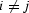 .Transforming the autocorrelation into the frequency domain
gives
.Transforming the autocorrelation into the frequency domain
gives ![$E[\overline{r(\omega)} r(\omega)] = 1$](img112.gif) ,where
,where 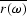 is the complex conjugate of
is the complex conjugate of 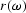 .Since
.Since  is the convolution of
is the convolution of 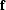 and
and  ,
,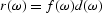 ,
,
| ![\begin{displaymath}
E[\overline{r(\omega)} r(\omega)] = 1 = E[ \overline{f(\omega) d(\omega)} f(\omega) d(\omega) ].\end{displaymath}](img116.gif) |
(28) |
Since the filter 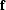 is a linear operator,
it can be taken outside of the expectationPapoulis (1984)
to make the previous expression become
is a linear operator,
it can be taken outside of the expectationPapoulis (1984)
to make the previous expression become
| ![\begin{displaymath}
\frac{1}{\overline{f(\omega)} f(\omega)} = E[\overline{ d(\omega)} d(\omega)].\end{displaymath}](img117.gif) |
(29) |
Thus, the power spectrum of 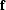 is the inverse of the power spectrum of
is the inverse of the power spectrum of  .Although the phase of the data
.Although the phase of the data
 is lost when creating the cross-correlation
of
is lost when creating the cross-correlation
of  to get
to get 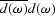 ,the phase of the filter is generally unimportant
when the filter is being used as an annihilation
filter in an inversion.
For applications where a minimum phase filter is required,
Kolmogoroff spectral factorizationClaerbout (1992a)
may be used.
,the phase of the filter is generally unimportant
when the filter is being used as an annihilation
filter in an inversion.
For applications where a minimum phase filter is required,
Kolmogoroff spectral factorizationClaerbout (1992a)
may be used.
Another way of expressing the unpredictability of  is
is ![$E[\sv r \sv r^{\dagger}] = \st I$](img119.gif) ,that is,
the expectation of
,that is,
the expectation of 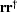 is the identity matrix.
This states that the expectation of the cross-terms of the errors are zero,
that is, the errors are uncorrelated.
This also states that the variances of the errors have equal weights.
To make the matrices factor
with an
is the identity matrix.
This states that the expectation of the cross-terms of the errors are zero,
that is, the errors are uncorrelated.
This also states that the variances of the errors have equal weights.
To make the matrices factor
with an 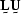 decomposition Strang (1988),
the expression
decomposition Strang (1988),
the expression 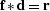 needs to be posed as a matrix operation
needs to be posed as a matrix operation 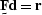 ,with
,with 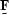 as an upper triangular matrix.
To do this,
the indices of
as an upper triangular matrix.
To do this,
the indices of
 and
and  are reversed from the usual order in their
vector representations.
A small example of
are reversed from the usual order in their
vector representations.
A small example of 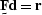 is
is
| 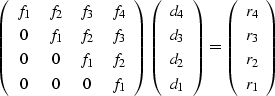 |
(30) |
Building one small realization of 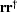 gives
gives
| 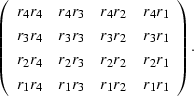 |
(31) |
To get an estimate of the expectation of this expression,
it must be remembered that the data series is stationary,
and the error will also be stationary.
Only the differences in the indices are important,
the locations are not.
It can be seen that the elements of (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
are the elements of the autocorrelation at various lags.
Using equation (
)
are the elements of the autocorrelation at various lags.
Using equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) makes the expectation of (
) makes the expectation of (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
become the identity matrix
)
become the identity matrix 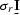 ,where the
,where the 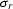 may be dropped, since it is only a scale factor
that may be incorporated into the filter or as a normalization of
the autocorrelation.
may be dropped, since it is only a scale factor
that may be incorporated into the filter or as a normalization of
the autocorrelation.
Starting from the expression ![$E[\sv r \sv r^{\dagger}] = \st I$](img119.gif) and substituting
and substituting
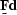 for
for  gives
gives
| ![\begin{displaymath}
E[ (\st F\sv d) (\st F\sv d)^{\dagger} ] =\st I\end{displaymath}](img127.gif) |
(32) |
or
| ![\begin{displaymath}
E[ \st F\sv d \sv d^{\dagger} \st F^{\dagger} ] =\st I.\end{displaymath}](img128.gif) |
(33) |
Once again, since 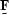 and
and 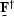 are linear operators,
they can be taken outside of the expectationPapoulis (1984)
are linear operators,
they can be taken outside of the expectationPapoulis (1984)
| ![\begin{displaymath}
\st F E[ \sv d \sv d^{\dagger}] \st F^{\dagger} =\st I.\end{displaymath}](img130.gif) |
(34) |
Moving the 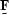 s to the right-hand side gives
s to the right-hand side gives
| ![\begin{displaymath}
E[ \sv d \sv d^{\dagger}] = \st F^{-1} (\st F^{\dagger})^{-1} = (\st F^{\dagger} \st F )^{-1}.\end{displaymath}](img131.gif) |
(35) |
Expanding one realization of a small example of ![$E[ \sv d \sv d^{\dagger}]$](img132.gif) gives
gives
| 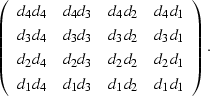 |
(36) |
Once again,
to get an estimate of the expectation of this expression,
it should be remembered that  is stationary,
and only the differences in the indices are important.
It can then be seen that E[di di-j] are elements of the autocorrelation,
and
is stationary,
and only the differences in the indices are important.
It can then be seen that E[di di-j] are elements of the autocorrelation,
and ![$E[ \sv d \sv d^{\dagger}]$](img132.gif) is the autocorrelation matrix of
is the autocorrelation matrix of  .Setting
.Setting ![$\st A = E[ \sv d \sv d^{\dagger}]$](img134.gif) gives
gives
| 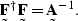 |
(37) |
Generally, ![$E[ \sv d \sv d^{\dagger}]$](img132.gif) will be invertible and positive definite
for real data.
There are some special cases where
will be invertible and positive definite
for real data.
There are some special cases where ![$E[ \sv d \sv d^{\dagger}]$](img132.gif) is not invertible
and positive definite, for example, when
is not invertible
and positive definite, for example, when  contains a single sine wave.
To avoid these problems, the stabilizer
contains a single sine wave.
To avoid these problems, the stabilizer 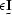 is often added to
the autocorrelation matrix,
where
is often added to
the autocorrelation matrix,
where  is a small number and
is a small number and 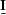 is the identity matrix.
In the geophysical industry, this is referred to as adding
white noise,
or whitening,
since adding
is the identity matrix.
In the geophysical industry, this is referred to as adding
white noise,
or whitening,
since adding 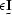 to the autocorrelation matrix
is equivalent to adding noise to the data
to the autocorrelation matrix
is equivalent to adding noise to the data  .
.
The matrix 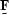 may be obtained from
the matrix
may be obtained from
the matrix 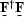 by Cholesky factorizationStrang (1988),
since
by Cholesky factorizationStrang (1988),
since 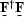 is symmetric positive definite.
Cholesky factorization factors a matrix into
is symmetric positive definite.
Cholesky factorization factors a matrix into 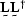 ,where
,where 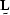 looks like
looks like
| 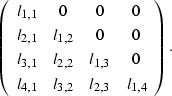 |
(38) |
The matrix 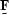 obtained from this factorization will be upper triangular,
as seen in (
obtained from this factorization will be upper triangular,
as seen in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
so the filter is seen to predict a given sample of
),
so the filter is seen to predict a given sample of  from the past samples,
and the maximum filter length is the length of the window.
This matrix could be considered as four filters of increasing length.
The longest filter, assuming it is the most effective filter,
could be taken as the prediction-error filter.
from the past samples,
and the maximum filter length is the length of the window.
This matrix could be considered as four filters of increasing length.
The longest filter, assuming it is the most effective filter,
could be taken as the prediction-error filter.
Another way of looking at this definition of a
prediction-error filter is to consider the filter
as a set of weights 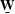 producing a weighted least-squares solution.
Following Strang 1986,
the weighted error
producing a weighted least-squares solution.
Following Strang 1986,
the weighted error 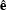 is
is 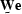 , where
, where 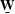 is to be determined, and
is to be determined, and  is the error of the original system.
The best
is the error of the original system.
The best 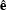 will make
will make
| ![\begin{displaymath}
E[ \hat{\sv e} \hat{\sv e}^{\dagger} ] = \st I.\end{displaymath}](img142.gif) |
(39) |
Since 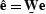 ,
,
| ![\begin{displaymath}
E[ \st W \sv e (\st W \sv e)^{\dagger} ] = \st W E[\sv e \sv e^{\dagger} ] \st W^{\dagger},\end{displaymath}](img144.gif) |
(40) |
where ![$E[\sv e \sv e^{\dagger} ]$](img145.gif) is the covariance matrix of
is the covariance matrix of  .Strang, quoting Gauss, says the best
.Strang, quoting Gauss, says the best 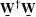 is the inverse
of the covariance matrix of
is the inverse
of the covariance matrix of  .Setting
.Setting 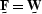 and
and 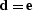 makes
the weight
makes
the weight 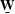 become the prediction-error filter
seen in equation (
become the prediction-error filter
seen in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
While I've neglected a number of issues,
such as the invertability of
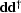 ,the finite length of
,the finite length of  ,
and the quality of the estimations of the expectations,
in practice the explicit solution to (
,
and the quality of the estimations of the expectations,
in practice the explicit solution to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
will not be used to calculate a prediction-error filter.
Most practical prediction-error filters will be calculated
using other, more efficient, methods.
A traditional method for calculating a short prediction-error filter
using Levinson recursion
will be shown in the next section.
In this thesis,
most of the filters are calculated using a conjugate-gradient technique
such as that shown in Claerbout 1992a.
)
will not be used to calculate a prediction-error filter.
Most practical prediction-error filters will be calculated
using other, more efficient, methods.
A traditional method for calculating a short prediction-error filter
using Levinson recursion
will be shown in the next section.
In this thesis,
most of the filters are calculated using a conjugate-gradient technique
such as that shown in Claerbout 1992a.
Most prediction-error filters are used as simple filters,
and the desired output is just the error  from the application
of the filter
from the application
of the filter 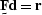 . Another use for these prediction-error filters is to describe
some class of information in an inversion,
such as signal or noise.
In this case, these filters are better described as
annihilation filters,
since the inversion depends on the condition that the filter applied
to some data annihilates, or zeros, a particular class of information
to a good approximation.
For example, a signal
. Another use for these prediction-error filters is to describe
some class of information in an inversion,
such as signal or noise.
In this case, these filters are better described as
annihilation filters,
since the inversion depends on the condition that the filter applied
to some data annihilates, or zeros, a particular class of information
to a good approximation.
For example, a signal  may be characterized by a signal annihilation
filter expressed as a matrix
may be characterized by a signal annihilation
filter expressed as a matrix 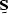 , so that
, so that 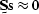 which may be expressed as
which may be expressed as 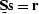 , where
, where  is small compared to
is small compared to  .A noise
.A noise  may be characterized by a noise annihilation
filter
may be characterized by a noise annihilation
filter 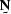 , so that
, so that 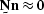 .Examples of annihilation filters used to characterize signal and noise
will be shown in chapters
.Examples of annihilation filters used to characterize signal and noise
will be shown in chapters ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
and
,
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
In this thesis, prediction-error filters will be referred to
as annihilation filters when used in an inversion context.
While prediction-error filters and annihilation filters
are used in different manners,
they are calculated in the same way.
In spite of the similarities in calculating the filters
involved, the use of these filters in simple filtering and in
inversion is quite different.
Simple filtering, whether one-, two-, or three-dimensional,
involves samples that are relatively close to the output point
and makes some simplifying assumptions.
An important assumption is
that the prediction error is not affected by the application of
the filter.
Inversion requires that the filters describe the data,
and the characterization of the data is less local than
it is with simple filtering.
The assumption that the prediction error is not affected by the filter
can be relaxed in inversion,
a topic to be further considered in chapters ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.





Next: An example of calculating
Up: Background and definitions
Previous: Solving methods
Stanford Exploration Project
2/9/2001
![]() contains no predictable information
may be expressed in several ways.
One method is by minimizing
contains no predictable information
may be expressed in several ways.
One method is by minimizing ![]() , where
, where ![]() is the conjugate transpose of
is the conjugate transpose of ![]() ,by calculating a filter that minimizes
,by calculating a filter that minimizes ![]() .This minimization reduces
.This minimization reduces ![]() to have the least energy possible,
where the smallest
to have the least energy possible,
where the smallest ![]() is assumed to
contain only unpredictable information.
is assumed to
contain only unpredictable information.
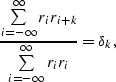
![]() .Transforming the autocorrelation into the frequency domain
gives
.Transforming the autocorrelation into the frequency domain
gives ![]() ,where
,where ![]() is the complex conjugate of
is the complex conjugate of ![]() .Since
.Since ![]() is the convolution of
is the convolution of ![]() and
and ![]() ,
,![]() ,
,
![]() is
is ![]() ,that is,
the expectation of
,that is,
the expectation of ![]() is the identity matrix.
This states that the expectation of the cross-terms of the errors are zero,
that is, the errors are uncorrelated.
This also states that the variances of the errors have equal weights.
To make the matrices factor
with an
is the identity matrix.
This states that the expectation of the cross-terms of the errors are zero,
that is, the errors are uncorrelated.
This also states that the variances of the errors have equal weights.
To make the matrices factor
with an ![]() decomposition Strang (1988),
the expression
decomposition Strang (1988),
the expression ![]() needs to be posed as a matrix operation
needs to be posed as a matrix operation ![]() ,with
,with ![]() as an upper triangular matrix.
To do this,
the indices of
as an upper triangular matrix.
To do this,
the indices of
![]() and
and ![]() are reversed from the usual order in their
vector representations.
A small example of
are reversed from the usual order in their
vector representations.
A small example of ![]() is
is
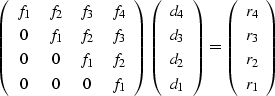
![]() gives
gives
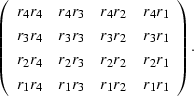
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
are the elements of the autocorrelation at various lags.
Using equation (
)
are the elements of the autocorrelation at various lags.
Using equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) makes the expectation of (
) makes the expectation of (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
become the identity matrix
)
become the identity matrix ![]() and substituting
and substituting
![]() for
for ![]() gives
gives
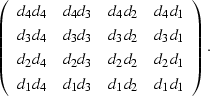
![]() will be invertible and positive definite
for real data.
There are some special cases where
will be invertible and positive definite
for real data.
There are some special cases where ![]() is not invertible
and positive definite, for example, when
is not invertible
and positive definite, for example, when ![]() contains a single sine wave.
To avoid these problems, the stabilizer
contains a single sine wave.
To avoid these problems, the stabilizer ![]() is often added to
the autocorrelation matrix,
where
is often added to
the autocorrelation matrix,
where ![]() is a small number and
is a small number and ![]() is the identity matrix.
In the geophysical industry, this is referred to as adding
white noise,
or whitening,
since adding
is the identity matrix.
In the geophysical industry, this is referred to as adding
white noise,
or whitening,
since adding ![]() to the autocorrelation matrix
is equivalent to adding noise to the data
to the autocorrelation matrix
is equivalent to adding noise to the data ![]() .
.![]() may be obtained from
the matrix
may be obtained from
the matrix ![]() by Cholesky factorizationStrang (1988),
since
by Cholesky factorizationStrang (1988),
since ![]() is symmetric positive definite.
Cholesky factorization factors a matrix into
is symmetric positive definite.
Cholesky factorization factors a matrix into ![]() ,where
,where ![]() looks like
looks like
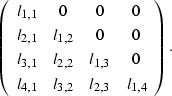
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
so the filter is seen to predict a given sample of
),
so the filter is seen to predict a given sample of ![]() producing a weighted least-squares solution.
Following Strang 1986,
the weighted error
producing a weighted least-squares solution.
Following Strang 1986,
the weighted error ![]() is
is ![]() , where
, where ![]() is to be determined, and
is to be determined, and ![]() is the error of the original system.
The best
is the error of the original system.
The best ![]() will make
will make
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![]() ,the finite length of
,the finite length of ![]() ,
and the quality of the estimations of the expectations,
in practice the explicit solution to (
,
and the quality of the estimations of the expectations,
in practice the explicit solution to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
will not be used to calculate a prediction-error filter.
Most practical prediction-error filters will be calculated
using other, more efficient, methods.
A traditional method for calculating a short prediction-error filter
using Levinson recursion
will be shown in the next section.
In this thesis,
most of the filters are calculated using a conjugate-gradient technique
such as that shown in Claerbout 1992a.
)
will not be used to calculate a prediction-error filter.
Most practical prediction-error filters will be calculated
using other, more efficient, methods.
A traditional method for calculating a short prediction-error filter
using Levinson recursion
will be shown in the next section.
In this thesis,
most of the filters are calculated using a conjugate-gradient technique
such as that shown in Claerbout 1992a.
![]() from the application
of the filter
from the application
of the filter ![]() . Another use for these prediction-error filters is to describe
some class of information in an inversion,
such as signal or noise.
In this case, these filters are better described as
annihilation filters,
since the inversion depends on the condition that the filter applied
to some data annihilates, or zeros, a particular class of information
to a good approximation.
For example, a signal
. Another use for these prediction-error filters is to describe
some class of information in an inversion,
such as signal or noise.
In this case, these filters are better described as
annihilation filters,
since the inversion depends on the condition that the filter applied
to some data annihilates, or zeros, a particular class of information
to a good approximation.
For example, a signal ![]() may be characterized by a signal annihilation
filter expressed as a matrix
may be characterized by a signal annihilation
filter expressed as a matrix ![]() , so that
, so that ![]() which may be expressed as
which may be expressed as ![]() , where
, where ![]() is small compared to
is small compared to ![]() .A noise
.A noise ![]() may be characterized by a noise annihilation
filter
may be characterized by a noise annihilation
filter ![]() , so that
, so that ![]() .Examples of annihilation filters used to characterize signal and noise
will be shown in chapters
.Examples of annihilation filters used to characterize signal and noise
will be shown in chapters ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
and
,
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.