![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
The real data examples in this chapter will involve prestack datuming,
but to provide insight as to how wave-equation datuming compares to
static shift, and for clarity of exposition, I will demonstrate
a few concepts using the zero-offset synthetic data
from Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a comparison of static shift and wave-equation
datuming applied to the same synthetic data displayed in
Figure
is a comparison of static shift and wave-equation
datuming applied to the same synthetic data displayed in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Although both methods
unravel the topographic distortion, the curvature of the diffracted
events is substantially different. This difference in curvature
is due to the inaccuracy of the static shift; in this situation
the assumption of vertical raypaths is invalid.
. Although both methods
unravel the topographic distortion, the curvature of the diffracted
events is substantially different. This difference in curvature
is due to the inaccuracy of the static shift; in this situation
the assumption of vertical raypaths is invalid.
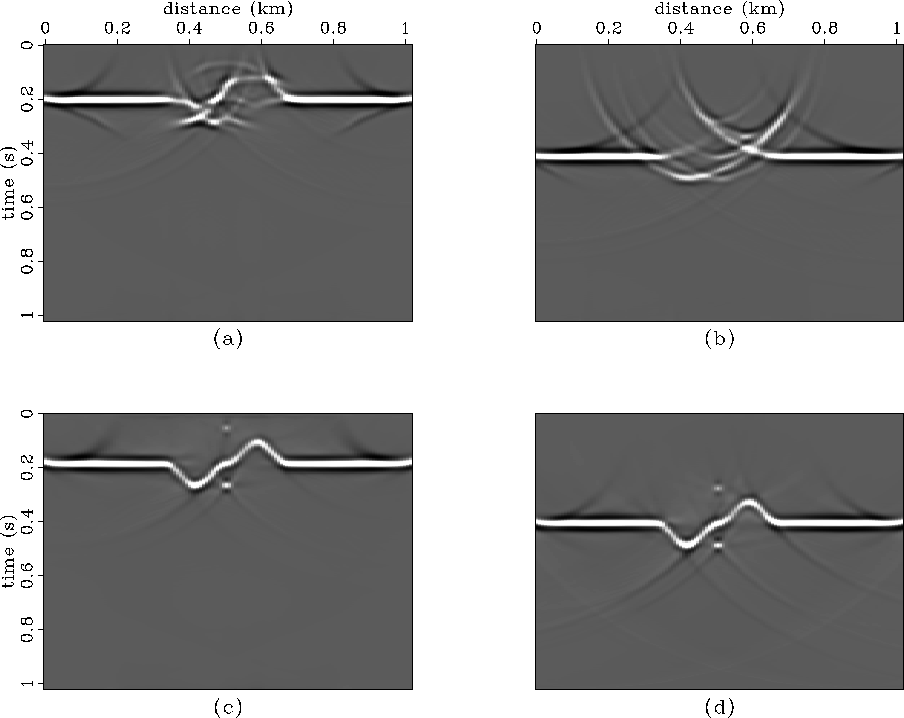
As mentioned earlier, detrimental effects
occur when wave-based processing is applied after an inappropriate
static shift. This is illustrated in the top two panels of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In this case, time-migration has been applied
after static shift downward in Figure
. In this case, time-migration has been applied
after static shift downward in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and after
static shift upward in Figure
a and after
static shift upward in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. In both cases, the
static shift has distorted the data so badly that migration fails.
A similar failure can be expected for any wave-based process
applied to prestack data. In this case, I define wave-based process
as any method which is built on the assumption that the data
obey the wave equation. This includes methods such as
normal-moveout correction (NMO),
dip-moveout correction (DMO),
NMO stack, prestack migration, and velocity analysis. This may partially
explain the common observation that DMO applied to overthrust data
often has detrimental effects
(Tilander and Mitchel, 1995; Burke and Knapp, 1995).
b. In both cases, the
static shift has distorted the data so badly that migration fails.
A similar failure can be expected for any wave-based process
applied to prestack data. In this case, I define wave-based process
as any method which is built on the assumption that the data
obey the wave equation. This includes methods such as
normal-moveout correction (NMO),
dip-moveout correction (DMO),
NMO stack, prestack migration, and velocity analysis. This may partially
explain the common observation that DMO applied to overthrust data
often has detrimental effects
(Tilander and Mitchel, 1995; Burke and Knapp, 1995).
When the data are extrapolated to the flat datum by wave-equation datuming,
the wavefield character of the data are preserved. This is demonstrated
in the lower panels of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) where the data have been
migrated after upward and downward continuation. Accurate images are
formed in both cases.
where the data have been
migrated after upward and downward continuation. Accurate images are
formed in both cases.
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b
and is reproduced here for ease of comparison.
b
and is reproduced here for ease of comparison.
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b
and
b
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b
and are reproduced here for ease of comparison.
b
and are reproduced here for ease of comparison.