




Next: Generalized formulation of wave-equation
Up: Wave-equation datuming operators
Previous: Phase-shift datuming with lateral
Finite-difference wave extrapolation is performed by transforming
the dispersion relation into a differential equation (Claerbout, 1985).
In 2-D, the dispersion relationship
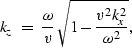
is converted to a differential equation by substituting
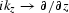 , to get
, to get
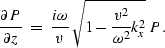
Muir's continued fraction expansion approximation to the square root and
the substitution 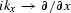 yields the
yields the 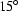 equation
equation
| 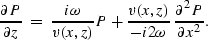 |
(22) |
Depth stepping proceeds by solution of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in two stages.
The first stage,
) in two stages.
The first stage,
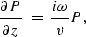
is solved analytically by
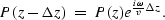
The second stage,
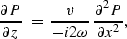
is solved by use of some method of finite differencing.
For a given depth step, 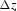 , the finite-difference extrapolation
is given by the product Di Li, where Di is a matrix representation
of the finite-difference solution method. In principle this could
be any solver, but in practice the examples in this dissertation are
solved using the Crank-Nicholson implicit method (Claerbout, 1985).
, the finite-difference extrapolation
is given by the product Di Li, where Di is a matrix representation
of the finite-difference solution method. In principle this could
be any solver, but in practice the examples in this dissertation are
solved using the Crank-Nicholson implicit method (Claerbout, 1985).
For the geometry of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , Li is the matrix
, Li is the matrix
![\begin{displaymath}
\left[
\begin{array}
{cccccc}
e^{i\frac{\omega}{v(x_1,z_i)...
...e^{i\frac{\omega}{v(x_6,z_i)} \Delta z} \\ \end{array}\right].\end{displaymath}](img83.gif)
Therefore, the upward continuation operator can be written as
| ![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{ccc}
D_3 L_3 D_2 L_2 D...
...]
\left[
\begin{array}
{c}
P(x,z_s,\omega)\end{array}\right],
}\end{displaymath}](img84.gif) |
(23) |
The adjoint algorithm is found by
transposing each matrix and reversing the multiplication order,
as follows:
| ![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{ccc}
A & B & C
\end...
...
\begin{array}
{c}
P(x,z_{\rm dat},\omega)\end{array}\right].
}\end{displaymath}](img85.gif) |
(24) |
Prestack finite-difference datuming can be performed
by extrapolation of shot and receiver gathers separately or
by implementation of the double square root equation,
![\begin{displaymath}
\frac{\partial P}{\partial z}\;=\;
\left[
\sqrt{
\left(\frac...
...ac{\partial^2}{\partial x_s^2}
}
\,\right]\,
P(x_s,x_g,\omega),\end{displaymath}](img86.gif)
and alternation between shot xs and group xg coordinates for
every depth step 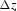 .
.





Next: Generalized formulation of wave-equation
Up: Wave-equation datuming operators
Previous: Phase-shift datuming with lateral
Stanford Exploration Project
2/12/2001
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in two stages.
The first stage,
) in two stages.
The first stage,
![]()
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , Li is the matrix
, Li is the matrix
![\begin{displaymath}
\left[
\begin{array}
{cccccc}
e^{i\frac{\omega}{v(x_1,z_i)...
...e^{i\frac{\omega}{v(x_6,z_i)} \Delta z} \\ \end{array}\right].\end{displaymath}](img83.gif)
![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{ccc}
D_3 L_3 D_2 L_2 D...
...]
\left[
\begin{array}
{c}
P(x,z_s,\omega)\end{array}\right],
}\end{displaymath}](img84.gif)
![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{ccc}
A & B & C
\end...
...
\begin{array}
{c}
P(x,z_{\rm dat},\omega)\end{array}\right].
}\end{displaymath}](img85.gif)
![\begin{displaymath}
\frac{\partial P}{\partial z}\;=\;
\left[
\sqrt{
\left(\frac...
...ac{\partial^2}{\partial x_s^2}
}
\,\right]\,
P(x_s,x_g,\omega),\end{displaymath}](img86.gif)