

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Chapter 1:
From prestack migration to migration to zero offset
Alexander M. Popovici
Author has no known email address
ABSTRACT
As a condition for further generalization of the migration
to zero-offset in variable velocity media,
I develop the theory for 2-D migration to zero offset (MZO)
in constant velocity media,
starting from prestack migration in midpoint-offset coordinates.
At the end of this chapter I arrive at an integral formulation
for the MZO operator, analytically derived from the double square
root (DSR) prestack migration equation. The integral formulation for
the MZO is very similar in form to the DSR equation, suggesting
a generalization to variable velocity media via a phase-shift
algorithm. Further chapters deal with offset separation and
the depth variable v(z) and laterally variable v(x,z) velocity
media.
|
Introducing the Double Square Root Equation
The theory for the double square root (DSR) equation
is discussed in detail in the first chapter of Yilmaz's (1979) thesis.
Without going into mathematical detail I will sketch
the path of the basic theory for obtaining the
DSR migration equation in offset and midpoint coordinates
starting from the wave equation. Readers familiar with
the DSR equation can skip directly to the next section.
The scalar wave equation in a 2-D medium of constant density
can be written as
| 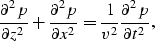 |
(1) |
where p=p(t,x,z) is the pressure field and v=v(x,z) is the earth
velocity.
The pressure field p(t,x,z) is a finite function and can be therefore
expressed as a double Fourier series
| 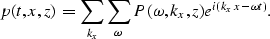 |
(2) |
Substituting equation (2) in equation (1) we obtain
| ![\begin{displaymath}
{\sum_{k_x} \sum_{\omega}[ {\partial^2 P(\omega,k_x,z) \over...
...a^2 \over v^2(x,z)} P(\omega,k_x,z)]
e^{i(k_x x-\omega t)}= 0}.\end{displaymath}](img3.gif) |
(3) |
Equation (3) should hold for any values of kx and  .This is possible only if each term inside the square parenthesis
is zero. This reasoning is similar to the condition that if
a polynomial is zero for any values of x, the coefficients of the
polynomial are zero.
Therefore we have
.This is possible only if each term inside the square parenthesis
is zero. This reasoning is similar to the condition that if
a polynomial is zero for any values of x, the coefficients of the
polynomial are zero.
Therefore we have
| 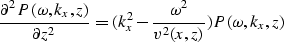 |
(4) |
valid for all values of kx and  .The problem is that in this form, the x-coordinate in the pressure
field is Fourier transformed and there is no direct
correspondence between a point (x,z) in the medium,
the velocity v(x,z), and the corresponding value of p(t,x,z)
at that location.
.The problem is that in this form, the x-coordinate in the pressure
field is Fourier transformed and there is no direct
correspondence between a point (x,z) in the medium,
the velocity v(x,z), and the corresponding value of p(t,x,z)
at that location.
For a constant velocity we write
| ![\begin{displaymath}
k_z=\left[{\omega^2 \over v^2}-{k_x^2 }\right]^{1 \over 2}\end{displaymath}](img6.gif) |
(5) |
where kz is constant for two given values of kx and  .Equation (5) is the well known dispersion
relation.
Equation (4) becomes an ordinary differential equation
.Equation (5) is the well known dispersion
relation.
Equation (4) becomes an ordinary differential equation
| 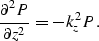 |
(6) |
For a constant kz equation (6) has the analytic solution
| 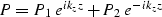 |
(7) |
To find the solution to equation (7) we would need to
have two initial or boundary conditions. We only
have the pressure field at z=0 as a boundary condition,
but we can still solve the problem if we decide to resolve
only the upgoing waves, in other words to use the exploding reflectors
principle.
If we know the
pressure field (or wavefield) at a certain depth we can
propagate it forward in time or backward in time. We
can also propagate it up in depth (along the z-axis) or down.
To understand how we determine the propagation direction
we have to analyze the values and
sign of kz.
The function
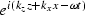
represents a plane wave.
If we ignore kx x, which determines the lateral variation,
we can introduce a function which we call phase(z,t) defined as
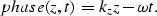
The phase is constant along a plane wave, and we write
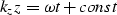
for the phase of a particular plane wave.
The plane wave is moving downward when kz has the
same sign with  because z increases with t
in order to keep the phase constant. So for the upward
moving waves we need to have opposite signs of kz and
because z increases with t
in order to keep the phase constant. So for the upward
moving waves we need to have opposite signs of kz and  (z is decreasing when t is increasing).
We have now figured out that in order to have only upgoing
waves we have to look at the sign of
(z is decreasing when t is increasing).
We have now figured out that in order to have only upgoing
waves we have to look at the sign of  and assign to
kz the opposite sign.
Therefore equation (7) becomes:
and assign to
kz the opposite sign.
Therefore equation (7) becomes:
| 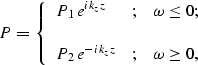 |
(8) |
which can be written in a compact form as:
| 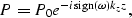 |
(9) |
where
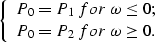
Setting z=0 in equation (9)
we identify P0 as the data recorded
at the surface:
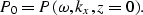
In this form we can use the data recorded at the surface
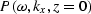 to propagate the wavefield to any depth level
to propagate the wavefield to any depth level
| 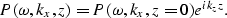 |
(10) |
The object of zero-offset migration is to estimate
P(t=0,kx,z) from P(t,kx,z=0).
Knowing the wavefield at any depth z0 we can
find the wavefield at any other depth z0+z.
For positive values of z we have
to propagate the wavefield back in time (toward t=0)
because we know that the wavefield travels upward.
If the known wavefield is at depth z0 and we want to
find the wavefield at depth z0-z, then we are
propagating the wavefield forward in time. This is the
direction we use for modeling.
However for depth varying velocity v(z) we have kz
approximately constant only
for small depth intervals (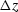 )
where we can consider the velocity constant.
Therefore equation (10) becomes
)
where we can consider the velocity constant.
Therefore equation (10) becomes
| 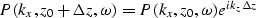 |
(11) |
and can be used to downward or upward extrapolate
the wave field for a small depth interval.
There are several restrictions on the values of kz. Equation
(6) has the solution (7) only for real
values of kz which imposes the condition
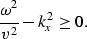
The solution represented in equation (10) is for
a single Fourier transform component of the wavefield.
The general solution
in time-space coordinates is obtained by summing all the
Fourier coefficients obtained from equation (10)
| 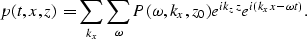 |
(12) |
In the case of a seismic experiment with many shots and receivers
we can downward continue separately the shots and the receivers
to any depth level.
The total phase shift to the same depth
level z becomes the phase shift of the
shots plus the phase shift of the receivers.
| ![\begin{displaymath}
k_z(\omega,k_g,k_s) z=
-{\rm sign}(\omega)\left[{\sqrt{{\ome...
...ver v^2} - k_g^2}+
\sqrt{{\omega^2 \over v^2} - k_s^2}}\right]z\end{displaymath}](img22.gif) |
(13) |
where ks and kg are the shot and receiver wavenumbers.
It is assumed here that the shots and geophones are on
a flat surface at zero depth z=0.
We can change the system of coordinates from shot and receiver to
midpoint and offset using the simple relations:
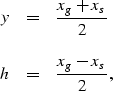
where y and h are respectively the midpoint and offset
coordinates, while xs and xg are the shot and geophone surface
coordinates. Note that the variable h represents half the
total distance between the source and geophone.
The total phase shift in the new wavenumber coordinates becomes
| ![\begin{displaymath}
k_z(\omega,k_y,k_h) z =
-{\rm sign}(\omega)\left[
{\sqrt{{\o...
...^2}+
\sqrt{{\omega^2 \over v^2}-({{k_y-k_h}\over2})^2}}\right]z\end{displaymath}](img24.gif) |
(14) |
where ky and kh are the midpoint and offset wavenumbers
and z represents the depth level to which the wavefield was
extrapolated.
This formulation allows a wavefield organized in midpoint-offset
coordinates to be downward continued to a certain depth level,
and it forms the basis for the prestack migration in
midpoint and offset coordinates shown in equation (15).
Isolating the Zero-offset migration
The basic concept for analytically deriving the MZO from prestack
migration is to separate the latter into two processes:
- Migration to zero offset.
- Zero-offset migration.
Once the zero-offset migration is extracted out of the
prestack migration operator, it is assumed that what is left
is in fact an operator which transforms the common-offset
data into zero-offset data, hence the name of the operator:
migration to zero offset.
I define the migration to zero offset as the operation that
converts a common-offset section into a zero-offset section.
For a constant velocity medium this is equivalent to the
sequence of normal moveout (NMO) followed by dip moveout (DMO).
We start with the constant velocity prestack migration
in offset-midpoint coordinates (Yilmaz, 1979) formulated as:
| 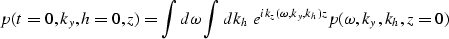 |
(15) |
where 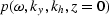 is the 3-D Fourier transform
of the field p(t,y,h,z=0) recorded at the surface, using
Claerbout's (1985) sign convention:
is the 3-D Fourier transform
of the field p(t,y,h,z=0) recorded at the surface, using
Claerbout's (1985) sign convention:
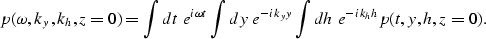
The phase 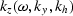 is defined in the
dispersion relation as
is defined in the
dispersion relation as
| ![\begin{displaymath}
{k_z(\omega,k_y,k_h)} \equiv
{ -{\rm sign}(\omega) \left[ \s...
...t{{\omega^2 \over v^2} -
{1 \over 4}(k_y-k_h)^2} \; \right] }.\end{displaymath}](img29.gif) |
(16) |
The two integrals in  and kh in equation (15)
represent the imaging
condition for zero offset and zero time (h=0,t=0).
and kh in equation (15)
represent the imaging
condition for zero offset and zero time (h=0,t=0).
The constant velocity zero-offset migration
(Gazdag, 1978) can be formulated as:
| 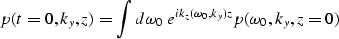 |
(17) |
where 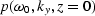 is the 2-D Fourier transform
of the field p(t,y,z=0).
The phase
is the 2-D Fourier transform
of the field p(t,y,z=0).
The phase 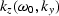 is defined in the
dispersion relation as
is defined in the
dispersion relation as
| 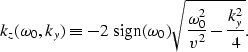 |
(18) |
In order to convert
equation (15) into a form similar to equation (17),
I use a change of variables from  to
to  such that after integrating over the
variable kh, equation (15) will be transformed
into the form:
such that after integrating over the
variable kh, equation (15) will be transformed
into the form:
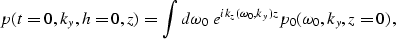
where 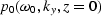 represents the zero-offset data field.
The rationale for casting the prestack migration equation in this
form is to identify the operations needed to obtain the zero-offset
field from the common-offset field. The assumption is that the
output of zero-offset migration and prestack-migration is the
same image. By dissecting the prestack-migration
and separating the zero-offset migration operator, we isolate
the migration to zero-offset (MZO) operator.
represents the zero-offset data field.
The rationale for casting the prestack migration equation in this
form is to identify the operations needed to obtain the zero-offset
field from the common-offset field. The assumption is that the
output of zero-offset migration and prestack-migration is the
same image. By dissecting the prestack-migration
and separating the zero-offset migration operator, we isolate
the migration to zero-offset (MZO) operator.
Using Hale's (1983) derivation,
a new variable  is introduced in order to
isolate the zero-offset migration operator. The expression for the
new variable
is introduced in order to
isolate the zero-offset migration operator. The expression for the
new variable  is found by equating the dispersion
relation for prestack migration to the dispersion relation
of zero offset migration,
is found by equating the dispersion
relation for prestack migration to the dispersion relation
of zero offset migration,
![\begin{displaymath}
-{2 \omega_0 \over v} \; \sqrt{
1-{{v^2k_y^2} \over {4 \omeg...
..._y+k_h)^2}+
\sqrt{1-{v^2 \over {4 \omega^2}}(k_y-k_h)^2}\right]\end{displaymath}](img37.gif)
and squaring the two equations twice. This algebra
is demonstrated in detail in Hale's thesis (1983), Appendix 3.A,
and therefore I did not repeat it here. The final
expression for the variable  is found to be
is found to be
| ![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4 \omega_0^2-v^2 k_y^2}} \right]}^{1 \over 2}},\end{displaymath}](img38.gif) |
(19) |
where  is considered variable and ky, kh are
constant.
Substituting
is considered variable and ky, kh are
constant.
Substituting  in equation (16),
the downward continuation phase
in equation (16),
the downward continuation phase 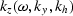 is transformed into
is transformed into
| 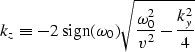 |
(20) |
which now has the same form as the phase in
equation (18). The somewhat lengthy but
straightforward algebraic
proof is shown in Appendix A.
In order to isolate the zero-offset
migration operator, after substituting the expression of
 given by equation (19) in the
prestack migration equation (15,
the order of integration is changed between
given by equation (19) in the
prestack migration equation (15,
the order of integration is changed between  and kh.
The integration
boundaries have to be observed carefully
as they are modified after each change of variables
and integration order. However, for the sake of simplicity, I will
ignore in the following demonstration the integration
limits, which are discussed in Appendix D.
and kh.
The integration
boundaries have to be observed carefully
as they are modified after each change of variables
and integration order. However, for the sake of simplicity, I will
ignore in the following demonstration the integration
limits, which are discussed in Appendix D.
By substituting the variable
 in equation (15)
with its new expression (19) as a function of
in equation (15)
with its new expression (19) as a function of  ,and changing the integration order between
,and changing the integration order between  and kh
the prestack migration equation becomes
and kh
the prestack migration equation becomes
| 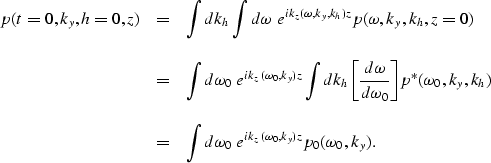 |
(21) |
The new field 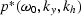 represents a remapping
(interpolation) from
represents a remapping
(interpolation) from  to
to  of the field
of the field 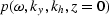 .Each value in the new field
.Each value in the new field 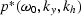 with
coordinates
with
coordinates 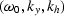 corresponds to the value
in the field
corresponds to the value
in the field 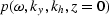 with coordinates
with coordinates
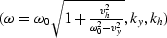 ,
where for simplicity I define the variables:
,
where for simplicity I define the variables:
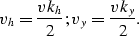
The field 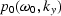 defined as
defined as
| ![\begin{displaymath}
p_0(\omega_0,k_y)=\int dk_h
{\left[{{d \omega} \over {d \omega_0}}\right]}
p^*(\omega_0,k_y,k_h)\end{displaymath}](img46.gif) |
(22) |
represents the zero-offset field.
The Jacobian in equation (22) obtained from the change of
coordinates from  to
to  is shown in Appendix B to be:
is shown in Appendix B to be:
| ![\begin{displaymath}
J = \displaystyle{{\left[{{d \omega} \over {d \omega_0}}\rig...
... [ 1 - {{v_h^2 v_y^2} \over
{ (\omega_0^2-v_y^2)^2}} \right ]}.\end{displaymath}](img47.gif) |
(23) |
The last equation in (21)
is of course the zero-offset migration equation (17),
the classic zero-offset downward
continuation and imaging described by Gazdag (1978)
or Stolt (1978).
Equation (22) represents a
way of obtaining the zero-offset section from
prestack data in midpoint-offset coordinates.
So far the operations needed to obtain the zero-offset
stacked section from the prestack field are:
- 1.
- Fourier transform the prestack field
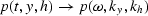 .
. - 2.
- Remap (interpolate) the data field from
 into
into  .
. - 3.
- Multiply by the Jacobian.
- 4.
- Integrate over kh.
- 5.
- Inverse Fourier transform
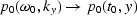 .
.
However I want to go further and replace the remapping step
with an operation that does not require the interpolation of the
initial data. The problem to be solved here is very similar
to the one confronted in Stolt migration. After our data
is evenly sampled by an FFT, we need to interpolate it
for a different variable.
MZO as phase shift
The interpolated field 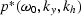 in equation (22)
represents the values of the
field
in equation (22)
represents the values of the
field 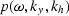 after remapping from
after remapping from  to
to
 . It is obtained by first Fourier transforming
the initial prestack field along all three
(time, midpoint and offset) axes:
. It is obtained by first Fourier transforming
the initial prestack field along all three
(time, midpoint and offset) axes:
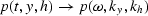 ,and second interpolating from
,and second interpolating from  to
to  .As in Stolt migration (Popovici et al. 1993),
we can replace the two steps of
.As in Stolt migration (Popovici et al. 1993),
we can replace the two steps of
- 1.
- Fourier transform with even sampling in
 ,
, - 2.
- interpolation from
 to
to  ,
,
by a single
step of slow Fourier transform with uneven sampling in  .We assume that the initial field is already Fourier transformed
in the offset and midpoint coordinates:
.We assume that the initial field is already Fourier transformed
in the offset and midpoint coordinates:
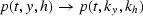 .
.
Formally we inverse Fourier transform in time equation (22)
to have
| 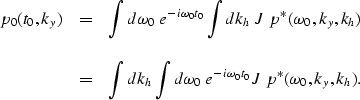 |
(24) |
In this formulation we can reinterpolate back from
 to
to  and drop the original remapping step.
For this, we change the integration variable from
and drop the original remapping step.
For this, we change the integration variable from  back to
back to  . The field
. The field 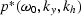 is
reverted to the original field
is
reverted to the original field 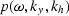 .In Appendix C the expression of
.In Appendix C the expression of  function of
function of
 is found to be
is found to be
| ![\begin{displaymath}
\omega_0 =
{1 \over 2}{\rm sign} (\omega)\left[
\sqrt{(\omega-v_y)^2-v_h^2}+\sqrt{(\omega+v_y)^2-v_h^2} \right].\end{displaymath}](img53.gif) |
(25) |
Substituting the variable  with the new expression in
with the new expression in  ,and simplifying the Jacobian in equation (24) we have
,and simplifying the Jacobian in equation (24) we have
| ![\begin{displaymath}
p_0(t_0,k_y)=
\int dk_h \int d\omega \; e^{-{i \over 2}\; {\...
...h^2}+\sqrt{(\omega+v_y)^2-v_h^2} \right]t_0}
p(\omega,k_y,k_h).\end{displaymath}](img54.gif) |
(26) |
Equation (26) represents a new form for migration to
zero offset. It is analytically derived from the wave equation
and therefore it handles correctly not only the kinematics of
the DMO+NMO operator, but also the amplitudes.
It is very similar in form to the DSR equation,
as the complex exponential
operator has the sum of two square roots in its phase.
However downward continuation is performed in time in the case
of the MZO operator and not in depth as is the case for DSR
migration. This in turn suggests the use of a VRMS velocity
in the case of variable velocity,
instead of the interval velocity, which could be a more convenient
process as the VRMS velocity is information obtained from surface
data and makes less assumptions about structure.
The only drawback so far to equation (26)
is that it performs a Fourier transform and later a
summation over the offset variable. I will show in the
next chapter how the offset variable can be separated and as a result
MZO can be applied to distinct common-offset sections.
Once MZO is applied to separate common-offset sections I
isolate the conventional NMO and DMO processes.
I will further show how equation (26) can be applied
to variable velocity media, via a phase shift algorithm similar
to Gazdag migration, and PSPI or split-step.
REFERENCES
- Claerbout, J. C., 1985, Imaging the Earth's Interior:
Blackwell Scientific Publications.
- Gazdag, J., 1978,
Wave equation migration with the phase shift method:
Geophysics, 43, 1342-1351.
- Gazdag, J., and Sguazzero, P., 1984,
Migration of seismic data by phase shift plus interpolation:
Geophysics, 49, 124-131.
- Hale, I. D., 1983, Dip-moveout by Fourier
transform: Ph.D. Thesis, Stanford University.
- Popovici, A. M., Blondel, P., & Muir, F., 1993,
Interpolation in Stolt migration:
SEP-79, 261-264.
- Stoffa, P. L., Fokkema, J. T., de Luna Freire, R. M.,
and Kessinger, W. P., 1990,
Split-step Fourier Migration:
Geophysics, 55, 410-421.
- Stolt, R.H., 1978,
Migration by Fourier transform:
Geophysics, 43, 23-48.
- Yilmaz, O.,1979, Prestack partial migration:
Ph.D. thesis, Stanford University.
- Zauderer, E., 1989,
Partial Differential Equations of Applied Mathematics:
Wiley-Interscience.
A
In this appendix I show that by writing the variable  function of
function of  , the double square-root (DSR) phase
used in prestack migration
is transformed to a new form corresponding to the
phase used for zero-offset migration.
The transformation from
, the double square-root (DSR) phase
used in prestack migration
is transformed to a new form corresponding to the
phase used for zero-offset migration.
The transformation from  to
to  as defined in equation (19) is:
as defined in equation (19) is:
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4...
...t[1 +
{{v_h^2} \over {\omega_0^2 -v_y^2}}\right]^{1 \over 2}},\end{displaymath}](img55.gif)
where vh and vy are defined as
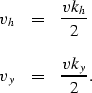
The DSR phase is transformed from
![\begin{displaymath}
{k_z(\omega,k_y,k_h)} \equiv
{ -{\rm sign}(\omega) \left[ \s...
...sqrt{{\omega^2 \over v^2} -
{1 \over 4}(k_y-k_h)^2} \right] },\end{displaymath}](img57.gif)
to
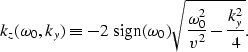
Hale (1983) in the Appendix A of his thesis
proves an equivalent assertion, with
a different logic. Comparing the DSR phase with the
phase of the zero-offset migration
(defined as a single square root), Hale finds the
expression of  which transforms the former into
the latter. I was tempted to refer
the reader to his appendix as an indirect proof,
but decided to include a thorough derivation, for completeness.
which transforms the former into
the latter. I was tempted to refer
the reader to his appendix as an indirect proof,
but decided to include a thorough derivation, for completeness.
Using the identity
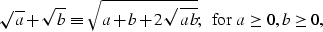
I rewrite the DSR phase as
| ![\begin{displaymath}
\begin{array}
{lcl}
k_z & = & \displaystyle{
-{1 \over v}{\r...
...2-v_y^2-v_h^2)^2-4v_y^2 v_h^2} \right]^{1 \over 2}}.\end{array}\end{displaymath}](img59.gif) |
(27) |
Examine the expression under the second square root (SSR)
in equation (27)
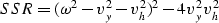
and substitute for  the expression in
the expression in  .The expression under the second square root becomes:
.The expression under the second square root becomes:
| ![\begin{displaymath}
\begin{array}
{lcl}
SSR & = & \displaystyle{
(\omega_0^2+{{\...
...-v_y^2 v_h^2} \over {\omega_0^2-v_y^2}}
\right]^2}.\end{array}\end{displaymath}](img61.gif) |
(28) |
The DSR becomes:
| ![\begin{displaymath}
\begin{array}
{lcl}
k_z & = & \displaystyle{
-{{\sqrt{2}} \o...
...eft[{\omega_0^2 \over v^2}-{k_y^2 \over 4} \right]},\end{array}\end{displaymath}](img62.gif) |
(29) |
which is the same equation as (18).
B
The purpose of this appendix is to evaluate the Jacobian of
the transformation from  to
to  :
:
![\begin{displaymath}
\begin{array}
{lcl}
J & = & \displaystyle{
{\left[{{d \omega...
..._h^2 v_y^2} \over
{ (\omega_0^2-v_y^2)^2}} \right]}.\end{array}\end{displaymath}](img63.gif)
Starting with the transformation of variable
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4...
...t[1 +
{{v_h^2} \over {\omega_0^2 -v_y^2}}\right]^{1 \over 2}},\end{displaymath}](img55.gif)
and differentiating we have
![\begin{displaymath}
\begin{array}
{lcl}
d\omega & = & \displaystyle{
\left\{ \le...
...^2} \over {(\omega_0^2-v_y^2)^2}} \right]d\omega_0},\end{array}\end{displaymath}](img64.gif)
and therefore the Jacobian is:
![\begin{displaymath}
J = {\left[{{d \omega} \over {d \omega_0}}\right]}=
(1+{{v_h...
...ft [ 1 - {{v_h^2 v_y^2} \over
{ (\omega_0^2-v_y^2)^2}} \right].\end{displaymath}](img65.gif)
C
The purpose of this appendix is to find the inverse of
the transformation 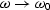 , or
to express
, or
to express  function of
function of  .Starting with the original transformation of variable
we have
.Starting with the original transformation of variable
we have
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4...
...t[1 +
{{v_h^2} \over {\omega_0^2 -v_y^2}}\right]^{1 \over 2}},\end{displaymath}](img55.gif)
and note that  has always the same sign as
has always the same sign as  .Square the equation to obtain
.Square the equation to obtain
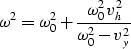
and after isolating the terms in  we have the equation
we have the equation
| 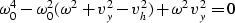 |
(30) |
which can be solved in 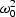 .The solutions are:
.The solutions are:
| 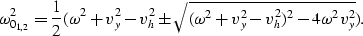 |
(31) |
The discriminant 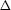 is
is
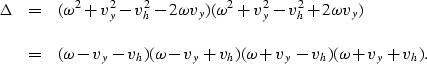
The existence conditions for kz
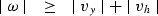
ensure that
 is always positive
and therefore
is always positive
and therefore  is always real within
the
is always real within
the  existence limits.
The choice of a positive sign for the discriminant
in equation (31) is assisted by the observation
that for vh=0, the case of a zero-offset data field,
the equation becomes an identity as it is expected.
Chosing the positive sign for the discriminant,
equation (31) becomes
existence limits.
The choice of a positive sign for the discriminant
in equation (31) is assisted by the observation
that for vh=0, the case of a zero-offset data field,
the equation becomes an identity as it is expected.
Chosing the positive sign for the discriminant,
equation (31) becomes
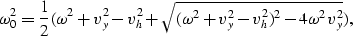
and using the observation that  has the same sign
as
has the same sign
as  we have:
we have:
| ![\begin{displaymath}
\omega_0 = {\rm sign} (\omega) \left[{1 \over 2}
(\omega^2+...
...mega^2+v_y^2-v_h^2)^2-4 \omega^2 v_y^2}})
\right]^{1 \over 2},\end{displaymath}](img75.gif) |
(32) |
which can be written in a simpler form using the identity
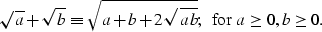
We have
| ![\begin{displaymath}
\begin{array}
{lcl}
\omega_0 & = & \displaystyle{
{\rm sign...
...+
\sqrt{({{2\omega} \over v}+k_y)^2-k_h^2} \right]}.\end{array}\end{displaymath}](img77.gif) |
(33) |
The second part of equation (33), in
a double square-root form, is of particular importance in
the phase of the MZO operator.
D
In this appendix I follow the integration boundaries for
all the integral transformations from equation (15)
to equation (26).
In equation (15) the values of the constant kz,
given by equation (16),
have to be real. This requires the conditions
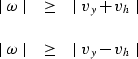
to be satisfied simultaneously.
Considering all four possible sign cases for
vy and vh represented
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and the interval of existence
for
, and the interval of existence
for  displayed in the shaded area,
the two requirements can be reduced to the condition
displayed in the shaded area,
the two requirements can be reduced to the condition
| 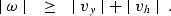 |
(34) |
DSRboundheight=2.5in,width=3.in.
Four possible cases for the values of vy and vh
and the interval of existence of  .
.
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the shaded area represents the
region of integration established by equation ((34)
for a constant ky.
khkyomegaheight=2.in,width=6.in.
Regions of integration.
The existence condition for vh in equation (34)
requires the integration boundaries in equation (15) to
be as follows:
the shaded area represents the
region of integration established by equation ((34)
for a constant ky.
khkyomegaheight=2.in,width=6.in.
Regions of integration.
The existence condition for vh in equation (34)
requires the integration boundaries in equation (15) to
be as follows:
![\begin{displaymath}
p(t=0,k_y,h=0,z)=
\int_{-\infty}^{\infty} \; d\omega
\int_{-...
...
{\mid {{2\omega} \over v} \mid - \mid k_y \mid} \; dk_h [...].\end{displaymath}](img80.gif)
After the change of variable from  to
to  in equation (19)
in equation (19)
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v_h^2 } \over
{ \omega_0^2-v_y^2}} \right]}^{1 \over 2}},\end{displaymath}](img81.gif)
we need to
determine the new integration boundaries.
In equation (21) the new variable
 takes values from
takes values from 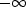 to
to 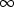 , but
the boundary values for kh have to be expressed now
function of the new variable
, but
the boundary values for kh have to be expressed now
function of the new variable  .Starting with the initial boundary equation (34)
and squaring it we have
.Starting with the initial boundary equation (34)
and squaring it we have
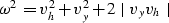
and replacing  with its expression in
with its expression in  we obtain
we obtain
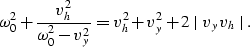
After multiplying by 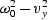 and grouping the terms
we have
and grouping the terms
we have
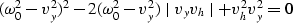
which is transformed in the condition for kh:
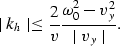
Therefore the second line in equation (21) should
have the integration boundaries:
![\begin{displaymath}
p(t=0,k_y,h=0,z)=
\int_{-\infty}^{\infty} \; d\omega_0
\int_...
...er v}{{\omega_0^2-v_y^2} \over {\mid v_y \mid}}} \;
dk_h [...],\end{displaymath}](img89.gif)
and subsequently equation (22) has the
same integration boundaries in kh
![\begin{displaymath}
p_0(\omega_0,k_y)=
\int_{-{2 \over v}{{\omega_0^2-v_y^2} \ov...
...er v}{{\omega_0^2-v_y^2} \over {\mid v_y \mid}}} \;
dk_h [...].\end{displaymath}](img90.gif)
Finally, the change of integration variable from  back to
back to  from equation (24)
to equation (26) will restore the initial condition
for kh:
from equation (24)
to equation (26) will restore the initial condition
for kh:
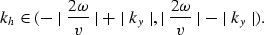
However, since in equation (26) there is an interchange
in the order of integration variables, the integration
boundaries become
![\begin{displaymath}
p(t_0,k_y)=
\int_{-\infty}^{\infty} \; dk_h
\int_{-{v \over ...
...{{v \over 2} (\mid k_y \mid + \mid k_h \mid)} \; d\omega [...].\end{displaymath}](img92.gif)


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
5/15/2001
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![\begin{displaymath}
{\sum_{k_x} \sum_{\omega}[ {\partial^2 P(\omega,k_x,z) \over...
...a^2 \over v^2(x,z)} P(\omega,k_x,z)]
e^{i(k_x x-\omega t)}= 0}.\end{displaymath}](img3.gif)
![]()
![]()
![]()
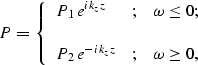
![]()
![]()
![]() )
where we can consider the velocity constant.
Therefore equation (10) becomes
)
where we can consider the velocity constant.
Therefore equation (10) becomes
![]()
![\begin{displaymath}
k_z(\omega,k_g,k_s) z=
-{\rm sign}(\omega)\left[{\sqrt{{\ome...
...ver v^2} - k_g^2}+
\sqrt{{\omega^2 \over v^2} - k_s^2}}\right]z\end{displaymath}](img22.gif)
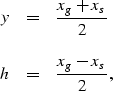
![\begin{displaymath}
k_z(\omega,k_y,k_h) z =
-{\rm sign}(\omega)\left[
{\sqrt{{\o...
...^2}+
\sqrt{{\omega^2 \over v^2}-({{k_y-k_h}\over2})^2}}\right]z\end{displaymath}](img24.gif)
![]()
![\begin{displaymath}
{k_z(\omega,k_y,k_h)} \equiv
{ -{\rm sign}(\omega) \left[ \s...
...t{{\omega^2 \over v^2} -
{1 \over 4}(k_y-k_h)^2} \; \right] }.\end{displaymath}](img29.gif)
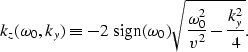
![]() to
to ![]() such that after integrating over the
variable kh, equation (15) will be transformed
into the form:
such that after integrating over the
variable kh, equation (15) will be transformed
into the form:
![]()
![]() is introduced in order to
isolate the zero-offset migration operator. The expression for the
new variable
is introduced in order to
isolate the zero-offset migration operator. The expression for the
new variable ![]() is found by equating the dispersion
relation for prestack migration to the dispersion relation
of zero offset migration,
is found by equating the dispersion
relation for prestack migration to the dispersion relation
of zero offset migration,
![\begin{displaymath}
-{2 \omega_0 \over v} \; \sqrt{
1-{{v^2k_y^2} \over {4 \omeg...
..._y+k_h)^2}+
\sqrt{1-{v^2 \over {4 \omega^2}}(k_y-k_h)^2}\right]\end{displaymath}](img37.gif)
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4 \omega_0^2-v^2 k_y^2}} \right]}^{1 \over 2}},\end{displaymath}](img38.gif)
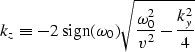
![]() given by equation (19) in the
prestack migration equation (15,
the order of integration is changed between
given by equation (19) in the
prestack migration equation (15,
the order of integration is changed between ![]() and kh.
The integration
boundaries have to be observed carefully
as they are modified after each change of variables
and integration order. However, for the sake of simplicity, I will
ignore in the following demonstration the integration
limits, which are discussed in Appendix D.
and kh.
The integration
boundaries have to be observed carefully
as they are modified after each change of variables
and integration order. However, for the sake of simplicity, I will
ignore in the following demonstration the integration
limits, which are discussed in Appendix D.
![]() in equation (15)
with its new expression (19) as a function of
in equation (15)
with its new expression (19) as a function of ![]() ,and changing the integration order between
,and changing the integration order between ![]() and kh
the prestack migration equation becomes
and kh
the prestack migration equation becomes
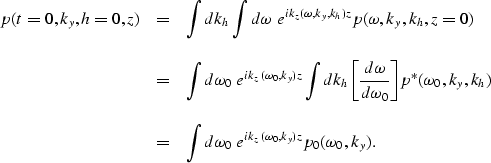
![]()
![\begin{displaymath}
J = \displaystyle{{\left[{{d \omega} \over {d \omega_0}}\rig...
... [ 1 - {{v_h^2 v_y^2} \over
{ (\omega_0^2-v_y^2)^2}} \right ]}.\end{displaymath}](img47.gif)
![]() in equation (22)
represents the values of the
field
in equation (22)
represents the values of the
field ![]() after remapping from
after remapping from ![]() to
to
![]() . It is obtained by first Fourier transforming
the initial prestack field along all three
(time, midpoint and offset) axes:
. It is obtained by first Fourier transforming
the initial prestack field along all three
(time, midpoint and offset) axes:
![]() ,and second interpolating from
,and second interpolating from ![]() to
to ![]() .As in Stolt migration (Popovici et al. 1993),
we can replace the two steps of
.As in Stolt migration (Popovici et al. 1993),
we can replace the two steps of
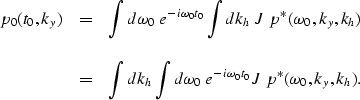
![]() function of
function of ![]() , the double square-root (DSR) phase
used in prestack migration
is transformed to a new form corresponding to the
phase used for zero-offset migration.
The transformation from
, the double square-root (DSR) phase
used in prestack migration
is transformed to a new form corresponding to the
phase used for zero-offset migration.
The transformation from ![]() to
to ![]() as defined in equation (19) is:
as defined in equation (19) is:
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4...
...t[1 +
{{v_h^2} \over {\omega_0^2 -v_y^2}}\right]^{1 \over 2}},\end{displaymath}](img55.gif)
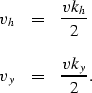
![\begin{displaymath}
{k_z(\omega,k_y,k_h)} \equiv
{ -{\rm sign}(\omega) \left[ \s...
...sqrt{{\omega^2 \over v^2} -
{1 \over 4}(k_y-k_h)^2} \right] },\end{displaymath}](img57.gif)
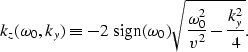
![]()
![\begin{displaymath}
\begin{array}
{lcl}
k_z & = & \displaystyle{
-{1 \over v}{\r...
...2-v_y^2-v_h^2)^2-4v_y^2 v_h^2} \right]^{1 \over 2}}.\end{array}\end{displaymath}](img59.gif)
![]()
![\begin{displaymath}
\begin{array}
{lcl}
SSR & = & \displaystyle{
(\omega_0^2+{{\...
...-v_y^2 v_h^2} \over {\omega_0^2-v_y^2}}
\right]^2}.\end{array}\end{displaymath}](img61.gif)
![\begin{displaymath}
\begin{array}
{lcl}
k_z & = & \displaystyle{
-{{\sqrt{2}} \o...
...eft[{\omega_0^2 \over v^2}-{k_y^2 \over 4} \right]},\end{array}\end{displaymath}](img62.gif)
![]() to
to ![]() :
:
![\begin{displaymath}
\begin{array}
{lcl}
J & = & \displaystyle{
{\left[{{d \omega...
..._h^2 v_y^2} \over
{ (\omega_0^2-v_y^2)^2}} \right]}.\end{array}\end{displaymath}](img63.gif)
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4...
...t[1 +
{{v_h^2} \over {\omega_0^2 -v_y^2}}\right]^{1 \over 2}},\end{displaymath}](img55.gif)
![\begin{displaymath}
\begin{array}
{lcl}
d\omega & = & \displaystyle{
\left\{ \le...
...^2} \over {(\omega_0^2-v_y^2)^2}} \right]d\omega_0},\end{array}\end{displaymath}](img64.gif)
![\begin{displaymath}
J = {\left[{{d \omega} \over {d \omega_0}}\right]}=
(1+{{v_h...
...ft [ 1 - {{v_h^2 v_y^2} \over
{ (\omega_0^2-v_y^2)^2}} \right].\end{displaymath}](img65.gif)
![]() , or
to express
, or
to express ![]() function of
function of ![]() .Starting with the original transformation of variable
we have
.Starting with the original transformation of variable
we have
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4...
...t[1 +
{{v_h^2} \over {\omega_0^2 -v_y^2}}\right]^{1 \over 2}},\end{displaymath}](img55.gif)
![]()
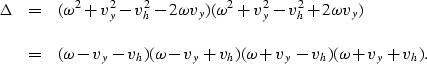
![]()
![]()
![]()
![\begin{displaymath}
\begin{array}
{lcl}
\omega_0 & = & \displaystyle{
{\rm sign...
...+
\sqrt{({{2\omega} \over v}+k_y)^2-k_h^2} \right]}.\end{array}\end{displaymath}](img77.gif)
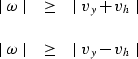
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and the interval of existence
for
, and the interval of existence
for ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the shaded area represents the
region of integration established by equation ((34)
for a constant ky.
khkyomegaheight=2.in,width=6.in.
Regions of integration.
The existence condition for vh in equation (34)
requires the integration boundaries in equation (15) to
be as follows:
the shaded area represents the
region of integration established by equation ((34)
for a constant ky.
khkyomegaheight=2.in,width=6.in.
Regions of integration.
The existence condition for vh in equation (34)
requires the integration boundaries in equation (15) to
be as follows:
![\begin{displaymath}
p(t=0,k_y,h=0,z)=
\int_{-\infty}^{\infty} \; d\omega
\int_{-...
...
{\mid {{2\omega} \over v} \mid - \mid k_y \mid} \; dk_h [...].\end{displaymath}](img80.gif)
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v_h^2 } \over
{ \omega_0^2-v_y^2}} \right]}^{1 \over 2}},\end{displaymath}](img81.gif)
![]()
![]()
![]()
![]()
![\begin{displaymath}
p(t=0,k_y,h=0,z)=
\int_{-\infty}^{\infty} \; d\omega_0
\int_...
...er v}{{\omega_0^2-v_y^2} \over {\mid v_y \mid}}} \;
dk_h [...],\end{displaymath}](img89.gif)
![\begin{displaymath}
p_0(\omega_0,k_y)=
\int_{-{2 \over v}{{\omega_0^2-v_y^2} \ov...
...er v}{{\omega_0^2-v_y^2} \over {\mid v_y \mid}}} \;
dk_h [...].\end{displaymath}](img90.gif)
![]() back to
back to ![]() from equation (24)
to equation (26) will restore the initial condition
for kh:
from equation (24)
to equation (26) will restore the initial condition
for kh:
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)