ifundefinedJimInclude

falsetrue

falsetrue

Constraints on minimum velocity variance in seismic traveltime tomography

James G. Berryman

Author has no known email address

ABSTRACT

Traveltime data together with known spacing between sources and receivers for seismic transmission tomography can be used to determine rigorous constraints on the minimum and maximum wave speeds in the propagating medium. These constraints lead to a new minimum variance criterion on inversion algorithms. These results do not improve the velocity reconstructions directly, but provide rigorous and easily computed figures of merit to help evaluate the difficulty of the reconstruction problem and the performance of tomographic inversion codes. Specifically, these criteria may be used during preprocessing to decide whether linear or nonlinear traveltime tomography methods are required for analyzing a given data set, or during postprocessing to determine whether regularization methods used to constrain the maximum model variance were overly restrictive.

INTRODUCTION

The degree of difficulty associated with inverting seismic traveltime data for wave speed distribution is largely determined by the contrasts present in the propagating medium. If velocity contrasts are small, seismic waves in a general refracting medium are only weakly bent and straight ray tomographic algorithms will give adequate results (Dines and Lytle, 1979; Lytle and Dines, 1980). If the velocity contrasts are large, then seismic waves are strongly refracted, implying that nonlinear tomography algorithms are required to invert such data. On the other hand, if the measurement configuration of sources and receivers has a severely limited range of view angles (as is often the case in crosswell geotomography), then the reconstruction will not place enough natural constraints (i.e., those derived from data) on the velocity model. In this situation, it is commonly observed that raw reconstructions (prior to regularization) produce wildly oscillating velocity distributions [see Berryman (1990)].

The large velocity fluctuations observed in raw reconstructions are often consequences of limited view angles in the measurement configuration. These velocity fluctuations are most often successfully controlled by applying some type of ``regularization method,'' which in almost all cases amounts to placing either global or local constraints on the range of variation of the model velocities. The actual constraints are usually only implicitly applied through some objective function that is minimized while the differences in the predicted versus measured traveltimes are also minimized. This process leads to a tradeoff between agreement with the traveltime data and consistency with either some smoothing condition or some other velocity variance constraint.

When no other information is available, it seems reasonable to apply regularization conditions as needed to prevent reconstructions from producing absurd results (Scales et al., 1990; Peng et al., 1993). However, if additional information is available in the data itself, then it seems clearly preferable (since no bias is introduced) to make use of all the constraints that may be inferred directly from the data before employing any ad hoc constraints. The author's paper on nonlinear traveltime tomography (Berryman, 1990) shows how Fermat's principle may be used to supply one important type of rigorous global constraint on the nonlinear inversion process. In the present paper, another type of constraint is derived based just on the geometry of the measurement configuration. This approach leads to two constraints that provide information about the absolute range of variation within the velocity field. And, because of the general nature of my argument, it actually provides a rigorous statement about the seismic speeds in the earth, not just in some special choice of model parametrization. I will call the total range of variation in the velocity field the velocity variance or the model variance, but there is no statistical information implied or contained in these constraints.

The constraints found in the next section show that the velocity variance must be at least as large as the apparent velocity variance for straight rays from the actual sources to the actual receiver positions. Such constraints are useful for deciding whether nonlinear tomography techniques are required in the inversion, or whether the choice of parameters used in particular regularization methods overly restrict the range of variation of the reconstructed model.

CONSTRAINTS ON MINIMUM VELOCITY VARIANCE

If the traveltime from a source at $\vec{x}_s$ to a receiver at $\vec{x}_r$is $t(\vec{x}_s,\vec{x}_r)$, then Fermat's principle of least time states that

$$\begin{eqnarray} t(\vec{x}_s,\vec{x}_r) = \min_{\{paths\}}\int_{path(\vec{x}_s,\... ...{x})\,dl^{path} = \int_{M(\vec{x}_s,\vec{x}_r)}s(\vec{x})\,dl^M, \end{eqnarray}$$ (1)

where $s(\vec{x})$ is the slowness (inverse of wave speed) throughout the propagating medium, and $M(\vec{x}_s,\vec{x}_r)$ is a minimizing path for the source/receiver pair $(\vec{x}_s,\vec{x}_r)$. My arguments are phrased most easily in terms of the wave slowness, but conversion to statements about wave velocity is easily accomplished at the end of these calculations.

Let $L(\vec{x}_s,\vec{x}_r)$ represent the straight line path from source to receiver and $d(\vec{x}_s,\vec{x}_r)$ the Euclidean distance from $\vec{x}_s$ to $\vec{x}_r$. Then, it follows that, if I perform the line integral in (1) along the straight-line path, the result is an upper bound on the measured traveltime, since

$$\begin{eqnarray} t(\vec{x}_s,\vec{x}_r) = \int_{M(\vec{x}_s,\vec{x}_r)}s(\vec{x})\,dl^M \le \int_{L(\vec{x}_s,\vec{x}_r)} s(\vec{x})\,dl^L. \end{eqnarray}$$ (2)

Furthermore, if $s_{max} \ge s(\vec{x})$ is the largest value of slowness anywhere in the model, I have

$$\begin{eqnarray} \int_{L(\vec{x}_s,\vec{x}_r)} s(\vec{x})\,dl^L \le s_{max}\int_{L(\vec{x}_s,\vec{x}_r)}dl^L = s_{max}d(\vec{x}_s,\vec{x}_r), \end{eqnarray}$$ (3)

since fixing the path and increasing all slownesses along the path up to the maximum value clearly produces an upper bound. Combining equations (2) and (3), I find

$$\begin{eqnarray} s_{max} \ge {{t(\vec{x}_s,\vec{x}_r)}\over{d(\vec{x}_s,\vec{x}_r)}}. \end{eqnarray}$$ (4)

Inequality (4) is true for all source/receiver pairs. As I consider all available data (i.e., all source/receiver pairs), I discover that the most restrictive information in (4) is provided by the largest right hand side. I give this most restrictive value the name Min(s_max) and summarize this result in the equation

$$\begin{eqnarray} s_{max} \ge Min(s_{max}) \equiv \max_{\{(\vec{x}_s,\vec{x}_r)\}} {{t(\vec{x}_s,\vec{x}_r)}\over {d(\vec{x}_s,\vec{x}_r)}}, \end{eqnarray}$$ (5)

stating that the maximum value of slowness is bounded below by Min(s_max).

Now I consider (1) again in order to obtain a similar constraint on $s_{min}\le s(\vec{x})$, the minimum value of slowness in the propagating medium. I find easily that

$$\begin{eqnarray} \int_{M(\vec{x}_s,\vec{x}_r)} s(\vec{x})\,dl^M \ge s_{min}\int_{M(\vec{x}_s, \vec{x}_r)} dl^M, \end{eqnarray}$$ (6)

since fixing the path and reducing all slownesses along that path to the minimum value produces a lower bound. Furthermore, the path length along the minimizing path clearly satisfies

$$\begin{eqnarray} \int_{M} dl^M \ge \int_{L} dl^L = d(\vec{x}_s,\vec{x}_r), \end{eqnarray}$$ (7)

since the straight line path has minimum path length. Combining equations (6) and (7), I find

$$\begin{eqnarray} t(\vec{x}_s,\vec{x}_r) \ge s_{min}d(\vec{x}_s,\vec{x}_r) \end{eqnarray}$$ (8)

for every source/receiver pair. Therefore, the minimum value of slowness is bounded above by

$$\begin{eqnarray} s_{min} \le Max(s_{min}) \equiv \min_{\{(\vec{x}_s,\vec{x}_r)\}} {{t(\vec{x}_s,\vec{x}_r)}\over {d(\vec{x}_s,\vec{x}_r)}}. \end{eqnarray}$$ (9)

I could have phrased these bounds in terms of the model velocity distribution $v(\vec{x}) = 1/s(\vec{x})$ using the same approach.

The conditions (5) and (9) are constraints on the minimum (not the maximum) variance of the slowness model, showing that fluctuations in model slowness must at least span the range [Max(s_min), Min(s_max)] and that the minimum and maximum of slowness must fall on the boundary or outside this range, so

$$\begin{eqnarray} s_{min} \le Max(s_{min}) \le Min(s_{max}) \le s_{max}. \end{eqnarray}$$ (10)

Equivalently the velocity minimum and maximum must fall on the boundary or outside the corresponding range

$$\begin{eqnarray} v_{min} \le Max(v_{min}) = 1/Min(s_{max}) \le 1/Max(s_{min}) = Min(v_{max}) \le v_{max}. \end{eqnarray}$$ (11)

It is important to emphasize that these constraints do not help in solving the inversion problem directly. (To solve the inverse problem, it would have been more helpful to obtain bounds on the maximum variation of the velocity instead, but unfortunately the minimum variation is what I can bound.) Rather they first provide a means (during preprocessing) of testing whether nonlinear traveltime tomography methods are required in the inversion. If I find that the contrast ratio

$$\begin{eqnarray} {\cal R}= {{Min(v_{max})-Max(v_{min})}\over{Max(v_{min})}} \end{eqnarray}$$ (12)

is greater than about 20%, then I expect bent rays to play an important role in the inversion for velocities (Dines & Lytle, 1979; Lytle & Dines, 1980). After completing some phase of an iterative model reconstruction, these constraints can then be applied as an intermediate or postprocessing step to check whether regularization methods employed to limit variance of the final velocity model were overly restrictive.

EXAMPLES

Synthetic examples

For purposes of testing algorithms, it is generally good practice to construct some representative synthetic models spanning the range of anticipated behavior. A suite of models was constructed in Berryman (1990) for purposes of testing reconstruction algorithms. The same models will be used here to test the minimum variance constraints.

All the models in the suite have $16\times 8$ square cells in 2D, while using 320 rays -- including 256 rays (16 sources $\times$ 16 receivers) from left to right (intended to mimic borehole-to-borehole data) and 64 rays (8 sources $\times$ 8 receivers) from top to bottom (surface-to-bottom data).

The traveltime data were generated with a bending method using the Nelder-Mead simplex search routine (Prothero et al., 1988; Nelder and Mead, 1965).

Three slowness models were considered. Each has a localized low speed anomaly near the top and a high speed anomaly near the bottom. The background velocity is normalized to unity ($v \equiv 1)$.The first example has $20\%$ anomalies; the second has $50\%$ anomalies; the third $100\%$ anomalies. The constraints are then computed from the synthetic traveltime data and the known distances from the sources to the receivers. The results are summarized in TABLE 1. I find that the constraints are indeed bounds as expected, but for these models they prove to be somewhat conservative estimates of the true range of the velocity variations.

1.2

TABLE 1.Synthetic examples based on the doublecross models in Berryman (1990).

Model v_min Max(v_min) Min(v_max) v_max # 1

Field example

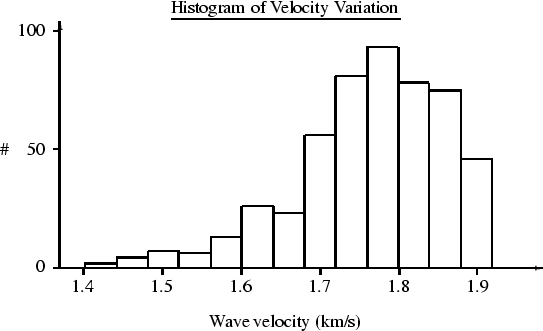
As an example using field data, I consider the Friendswood data set acquired by Chen et al. (1990) at Exxon. Using a representative subset of the measured traveltime data for 512 of the known source/receiver locations, I find (without actually inverting the data) the distribution of the velocity ratio d/t given in Figure 1. These data were collected near Friendswood, Texas, and included both crosswell data between two 304.8 m (1000 ft) cased boreholes separated by 182.9 m (600 ft), and vertical seismic profiling data with sources in one of the boreholes and receivers at the surface. Additional data were collected using surface sources and downhole receivers; however, we have not used this part of the data here because of some uncertainties in the locations of the surface sources.

Figure 1 shows that the minimum variance for this model should lie in the range 1.4-2.0 km/s (4600-6400 ft/s). Published reconstructions of the data obtained by Chen et al. (1990), Zhou et al. (1993), and also unpublished reconstructions by the author using the methods outlined in Berryman (1990) show the range of velocities to be 1.2-2.3 km/s (4000-7500 ft/s) for this region, consistent with the predictions inferred from Figure 1.

The Friendswood example shows clearly that, since the minimum variance in the slowness model for the data lies in the range 1.4-2.0 km/s (4600-6400 ft/s) -- corresponding to about 40% minimum contrast, inversion of this data set requires nonlinear traveltime tomography methods.

For this particular data set, wave speed variance information could also have been obtained from acoustic log data available at the Friendswood location. However, it is still useful to know that this wave speed variance information is also present in the traveltime data itself, since it can happen in practice that such acoustic log data are not always readily available.

 

Figure 1: Histogram of the number of occurrences of velocity values within a specified range of values for a representative subset of the Friendswood data set (Chen et al., 1990).

DISCUSSION

The analysis presented so far has ignored a number of potential complications. Two commonly noted issues in tomographic reconstructions are: (1) two-dimensional analysis versus three-dimensional earth and (2) isotropic analysis versus anisotropic earth. The simplicity of the present approach has the advantage that these two complications do not affect my results -- straight lines are still straight lines in three-dimensions while minimum and maximum speeds are still minimum and maximum speeds in anisotropic media. Thus, these cases are actually implicitly included in the analysis. Similarly, multipathing is also included since the straight line path is still the shortest path between source and receiver, regardless of the presence of alternative paths.

However, noise in the traveltime data can have more serious effects on our arguments. Two types of noise should be distinguished: (1) simple picking errors due to discrete time sampling and (2) more subtle errors due to picking first energetic arrivals rather than true first arrivals (which may be too low in amplitude to pick). Simple picking errors (assumed to be on the order of the time sample rate of the recorded seismic data) affects the calculated values by at most a few percent (except for cases with very high velocities or very small well spacing). When averaged over all view angles, I should still get reasonable estimates of the minimum variance of the velocities using these constraints. On the other hand, if first energetic arrivals have been picked rather than first arrivals, then a systematic bias is introduced, shifting traveltimes to higher values and velocities to lower values. But, if these errors are at least reasonably consistent, I should still obtain a valid estimate of the relative range of the velocity variance, even though the absolute range may be significantly in error. Such difficulties should not decrease the usefulness of the proposed figures of merit. It is only the relative range of variance that is important for deciding whether to use nonlinear inversion techniques. Similarly, in many regularization methods, it is only the relative rather than the absolute variance that is constrained.

CONCLUSIONS

On the one hand, large velocity contrasts in the propagating medium are the cause of nonlinearity in the inversion. On the other hand, large velocity contrasts in the reconstructed model can be an effect of limited view angles available in the data, when inadequate regularization has been applied in the inversion scheme. In either case, the velocity variance is a key characteristic of the model, so any information I can obtain to quantify this factor should prove useful.

I have shown that rigorous constraints on the range of variation in the seismic velocities in the earth may be obtained from traveltime data and source/receiver geometry, with no need for extensive processing of the data using a tomographic reconstruction code. These constraints determine the minimum variance in model wave speeds that may be expected if a reconstruction is performed. Furthermore, these results provide handy clues to the necessity (or lack of necessity) of using nonlinear reconstruction codes to perform the data inversion.

The results presented provide rigorous and easily computed figures of merit based only on the data to help evaluate the difficulty of the reconstruction problem and the performance of tomographic inversion codes.

ACKNOWLEDGMENTS

I thank S.-Y. Lu for assistance in acquiring and using the Exxon Friendswood data set, and S. T. Chen, S. Blakeslee, and the management of Exxon for making the data available. I thank T. Rekdal for detailed comments on the manuscript.

REFERENCES

• Berryman, J. G., 1990, Stable iterative reconstruction algorithms for nonlinear traveltime tomography: Inverse Problems 6, 21-42.
• Chen, S. T., Zimmerman, L. J., & Tugnait, J. K., 1990, Subsurface imaging using reversed vertical seismic profiling and crosshole tomographic methods: Geophysics 55, 1478-1487.
• Dines, K. A. & Lytle, R. J., 1979, Computerized geophysical tomography: Proc.IEEE 67, 1065-1073.
• Lytle, R. J. & Dines, K. A., 1980, Iterative ray tracing between boreholes for underground image reconstruction: IEEE Trans.Geosci.Remote Sens. 18, 234-240.
• Nelder, J. A., & Mead., R., 1965, A simplex method for function minimization: Computer J. 7, 308-313.
• Peng, C., Rodi, W., & Toksöz, M. N., 1993, Smoothest-model reconstruction from projections: Inverse Problems 9, 339-354.
• Prothero, W. A., Taylor, W. J., & Eickemeyer, J. A., 1988, A fast, two-point, three-dimensional raytracing algorithm using a simple step search method: Bull.Seismol.Soc.Am. 78, 1190-1198.
• Scales, J. A., Docherty, P., & Gersztenkorn, A., 1990, Regularization of nonlinear inverse problems: Imaging the near-surface weathering layer: Inverse Problems 6, 115-131.
• Zhou, C., Cai, W., Luo, Y., Schuster, G., & Hassanzadeh, S., 1993, High-resolution cross-well imaging by seismic traveltime + waveform inversion: The Leading Edge 12, 988-991.