![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
ABSTRACTA significant degradation in the quality of Kirchhoff 3-D migration images often arises because the migration operator summation trajectory is too steep for the input seismic trace spacing and frequency content. We present an operator anti-aliasing method that suppresses this problem, based on local triangle filtering. The N-point anti-alias triangles are efficiently applied as 3-point filters after causal and anticausal integration of the seismic trace data. We implement our method on a massively parallel CM-5 in a memory and floating-point efficient algorithm, and compare our anti-aliasing method to a standard Kirchhoff migration using a 3-D salt intrusion dataset from the Gulf of Mexico. Our results indicate that our anti-aliasing method greatly enhances the 3-D resolution of steep salt-sediment interfaces and faults, and suppresses false reflections caused by conventional Kirchhoff-migration aliasing artifacts. |
INTRODUCTION The process of seismic migration involves a mapping of the input seismic trace data by a migration operator to the output structural image. Spatial aliasing of the migration process can be problematic in all three domains: data, operator and image. These three types of spatial aliasing are distinct and independent, although they are often confused.
Aliasing defined
Data aliasing occurs when there are seismic frequencies f and
dips ![]() along reflection and
diffraction events in recorded seismic data which violate the following
criterion:
along reflection and
diffraction events in recorded seismic data which violate the following
criterion: ![]() . The term fd is the
maximum unaliased
frequency in the data for a given trace spacing
. The term fd is the
maximum unaliased
frequency in the data for a given trace spacing ![]() , a velocity vr
at the receiver location, and a local plane-wave incident angle
, a velocity vr
at the receiver location, and a local plane-wave incident angle
![]() at the recording surface. Once data have been aliased during the
recording process, it is difficult to avoid subsequent processing
artifacts except by reshooting the survey at a finer group spacing,
or by trying to interpolate the original data without interpolating
the aliases, e.g., Spitz (1991) and Claerbout (1992).
Yilmaz (1988) gives a good overview of data aliasing and its
effects on all methods of migration.
at the recording surface. Once data have been aliased during the
recording process, it is difficult to avoid subsequent processing
artifacts except by reshooting the survey at a finer group spacing,
or by trying to interpolate the original data without interpolating
the aliases, e.g., Spitz (1991) and Claerbout (1992).
Yilmaz (1988) gives a good overview of data aliasing and its
effects on all methods of migration.
Image aliasing occurs when the output sampling of the image space is too coarse to properly represent migrated dips. In the case of Kirchhoff migration, image aliasing is mostly a cosmetic problem and can be remedied by choosing an appropriate image mesh upon which to estimate the migrated structural image. Note that the Kirchhoff-migrated values at each mesh point in an aliased image space are uncontaminated and correct (assuming no data or operator aliasing). For example, a single migrated output trace at a well location may be entirely accurate without having to estimate any adjacent migrated traces. This ``target-oriented'' capability of Kirchhoff migration is not possible with spectral or finite-difference migration methods. Kirchhoff image aliasing may be a problem, however, if the migrated image is needed as input to subsequent multi-channel processing.
Operator aliasing occurs when the operator dip along the migration summation trajectory is too steep for a given input seismic trace spacing and frequency content. Spatial aliasing of Kirchhoff integral operators is likely because the operators are designed in the discrete space-time domain rather than the spectral domain. Great care must be taken to ensure that the f-k spectrum of a given space-time operator contains no aliased energy wrapped beyond the Nyquist frequency and wavenumbers. This implies that space-time operators which are spatially undersampled and contain significant steep-dip and high-frequency energy are likely to suffer from severe operator aliasing. In contrast, migration operators designed explicitly in the f-k domain are unaliased by definition, and operators designed in the f-x domain are easily modified to suppress spatial aliasing.
Previous work Conventionally, anti-aliasing of Kirchhoff operators can be partially accomplished by trace interpolation, aperture control, and operator dip filtering. Trace interpolation decreases the spatial sample interval and thus increases the spatial Nyquist frequency, but at the potentially prohibitive cost of increasing the total 3-D migration input load (e.g., Yilmaz, 1988). Migration aperture-control and operator dip-filtering have the effect of suppressing aliased steep-dip contributions to the output image. Unfortunately, these suppressed steep dips may be precisely the events of interest when imaging near-vertical structure such as salt flanks and faults.
Hale (1991) proposed a method to anti-alias Kirchhoff dip-moveout (DMO) operators by replicating time-shifted versions of the input seismic traces to approximate a summation along an equal-time-sampled version of the operator. Hale's subsequent nearest-neighbor spatial interpolation implies a boxcar averaging of the input trace values along the time direction, whereas we use triangle filtering to increase accuracy at steep migration dips. Hale's test of summing DMO impulse responses and matching the result to the original impulse ensures both operator aliasing and image aliasing are suppressed, which may invoke more lowpass-filtering and loss of resolution than is strictly necessary for the case of migration operator anti-aliasing alone. Hale's replication of time-shifted input traces and spatial interpolations may be inefficient from both a floating-point and memory perspective for 3-D migration algorithms, such as ours, that process thousands of traces simultaneously.
Gray (1992) proposed an approximate but cost-effective method to anti-alias Kirchhoff migration operators by performing aperture-dependent lowpass temporal filtering of the input trace data. He suggested that approximately three copies of the input data be lowpass-filtered at different high-cut frequencies. During migration the wide-aperture portions of the migration operator would be drawn increasingly from the lowest-frequency-content filtered trace copies. This corresponds to the notion that the wide-aperture portions of the migration operator have the steepest dips and therefore only the lowest frequencies will be unaliased. Our method is more accurate because we calculate the complete vector of high-cut frequencies separately for each diffraction trajectory, and design and apply our anti-alias filters on the fly accordingly. Our method is as cost-effective as Gray's approach, but does not require the memory-intensive storage of multiple data copies to implement the anti-aliasing.
We present an improved method for anti-aliasing Kirchhoff migrations. We first derive the relevant operator aliasing criteria and then present our efficient method of anti-aliasing the migration operator by local triangle filtering of the seismic trace. Finally, we compare applications of our anti-aliased Kirchhoff migration to conventional aperture-weighted Kirchhoff migration on a 3-D marine seismic data example.
ANTI-ALIASING THEORY The operator anti-aliasing criterion defines the maximum unaliased temporal frequency in the seismic data at the location that the operator trajectory intercepts a seismic trace, and is a function of the local operator dip and the trace spacing. In order to remain unaliased, the sequence of seismic trace samples summed along the operator trajectory must satisfy the dip Nyquist sampling criterion:
| |
(1) |
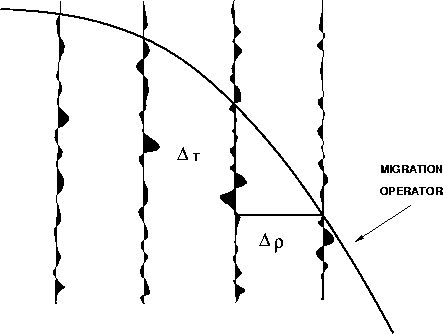
The geometry of the operator anti-aliasing criterion is depicted in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The factor
.
The factor ![]() is the moveout time along the migration operator
between adjacent traces.
The term
is the moveout time along the migration operator
between adjacent traces.
The term ![]() is the local spatial derivative of the migration
operator trajectory at the point of intersection with the seismic trace, and
is the local spatial derivative of the migration
operator trajectory at the point of intersection with the seismic trace, and
![]() is the seismic trace spacing along the recording surface.
The anti-aliasing criterion (1) suggests
local lowpass filtering of the seismic trace to ensure that
frequencies larger than fmax are not incorrectly migrated into the
output image. As discussed later, we implement the anti-aliasing lowpass
filtering efficiently and robustly with local triangle filters.
is the seismic trace spacing along the recording surface.
The anti-aliasing criterion (1) suggests
local lowpass filtering of the seismic trace to ensure that
frequencies larger than fmax are not incorrectly migrated into the
output image. As discussed later, we implement the anti-aliasing lowpass
filtering efficiently and robustly with local triangle filters.
 |
Kirchhoff time migration
It is instructive to evaluate the anti-aliasing criterion for the
special case of Kirchhoff time migration, which can be
extended to the case of Kirchhoff depth migration.
For time migration, we derive an
expression for the anti-aliasing criterion (1)
by analytically evaluating the operator derivative term ![]() .We begin by considering the analytic expression of the Kirchhoff 3-D
prestack time migration operator, which has the form
.We begin by considering the analytic expression of the Kirchhoff 3-D
prestack time migration operator, which has the form
| |
(2) |
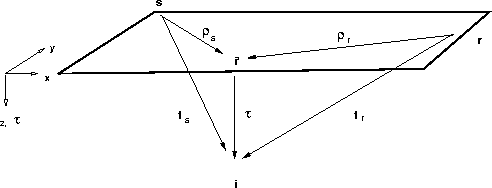
As shown in the geometry of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the term tk=ts + tr is the total two-way Kirchhoff migration
reflection traveltime,
,
the term tk=ts + tr is the total two-way Kirchhoff migration
reflection traveltime,
![]() is the one-way vertical traveltime or pseudo-depth
to the reflection point, and v is the rms migration velocity that
varies as a function of surface location and pseudo-depth
is the one-way vertical traveltime or pseudo-depth
to the reflection point, and v is the rms migration velocity that
varies as a function of surface location and pseudo-depth ![]() .The lengths
.The lengths ![]() and
and ![]() are the distances measured along the
planar recording surface between the source or receiver, respectively,
to the vertical projection of the image point on the recording
surface, expressed as
are the distances measured along the
planar recording surface between the source or receiver, respectively,
to the vertical projection of the image point on the recording
surface, expressed as
| |
(3) |
Equation (3) assumes that the recording surface is a horizontal plane
at a constant datum depth z0.
The subscript ![]() is a wildcard for either the source or receiver
coordinate subscripts s and r, and the subscript i
refers to the surface location of the subsurface image point projected up
onto the recording surface.
is a wildcard for either the source or receiver
coordinate subscripts s and r, and the subscript i
refers to the surface location of the subsurface image point projected up
onto the recording surface.
 |
The spatial derivative of (2) is needed to determine the migration operator aliasing criterion, which can be derived as
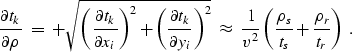 |
(4) |
We evaluate the effective rms spatial sampling interval ![]() for the prestack migration operator as
for the prestack migration operator as
| |
(5) |
where we define ![]() and
and ![]() in the prestack case as
in the prestack case as
| |
(6) |
| |
(7) |
The terms ![]() and
and ![]() are the true inline and crossline sampling
intervals of the seismic trace data, and are assumed to be regular
but possibly unequal in length. A more complicated analysis is
required for irregular trace spacings, which this paper does
not address.
are the true inline and crossline sampling
intervals of the seismic trace data, and are assumed to be regular
but possibly unequal in length. A more complicated analysis is
required for irregular trace spacings, which this paper does
not address.
Given the analytic expressions for the spatial derivative of the
Kirchhoff time migration operator ![]() ,
and the definition of the areal trace spacing interval
,
and the definition of the areal trace spacing interval ![]() ,
we derive an analytic expression for the time migration
operator anti-aliasing criterion. For the prestack case, the
anti-aliasing criterion is
,
we derive an analytic expression for the time migration
operator anti-aliasing criterion. For the prestack case, the
anti-aliasing criterion is
| |
(8) |
where the prestack definition of ![]() given by (5) -
(7) must be used.
given by (5) -
(7) must be used.
Kirchhoff depth migration In contrast to the time migration method above, the depth migration anti-aliasing criterion does not have a general analytic solution. Kirchhoff depth migration operators in v(x,y,z) media do not have simple hyperbolic forms, and must be evaluated numerically in heterogeneous migration velocity models. However, we propose three methods to provide satisfactory depth migration anti-aliasing results.
The first and most straightforward method is simply to use the
rms velocity field v and the time migration anti-aliasing criterion
(8), of the previous section,
to design the anti-aliasing lowpass filters along the non-hyperbolic
depth migration operators. This approach is robust because the dip along
the time migration operator is a reasonable approximation to the average
dip ![]() along the true depth migration trajectory.
along the true depth migration trajectory.
The second depth migration anti-aliasing technique applies to
Kirchhoff depth migration driven by traveltime tables. In this
case, the operator derivative ![]() in the general
anti-aliasing criterion (1) can be evaluated by differencing
the source and receiver traveltimes at the trace location with respect
to an adjacent source and receiver location. This approach is more
accurate than the time migration approximation, but requires extra
memory and I/O overhead to load the adjacent traveltime tables,
or extra computation time if the adjacent traveltimes are interpolated
from a sparse set of traveltime tables already loaded into memory.
in the general
anti-aliasing criterion (1) can be evaluated by differencing
the source and receiver traveltimes at the trace location with respect
to an adjacent source and receiver location. This approach is more
accurate than the time migration approximation, but requires extra
memory and I/O overhead to load the adjacent traveltime tables,
or extra computation time if the adjacent traveltimes are interpolated
from a sparse set of traveltime tables already loaded into memory.
The third depth migration anti-aliasing technique applies to
Kirchhoff depth migration in which the traveltime values are
computed by raytracing on the fly. In this case, an extra set
of rays can be traced from adjacent source and receiver
locations down to all subsurface points, or interpolated
from a single set of dynamic rays by paraxial interpolation.
Then the difference in ray arrival times can be used to approximate the
operator derivative ![]() in (1). This method is
more computationally intensive than the traveltime table approach,
but has significantly smaller memory requirements.
in (1). This method is
more computationally intensive than the traveltime table approach,
but has significantly smaller memory requirements.
In the sections that follow, we assume that the operator derivative
![]() of equation (1) is a known quantity,
whether for time or depth migration, since it can be calculated by any
of the three methods described above.
of equation (1) is a known quantity,
whether for time or depth migration, since it can be calculated by any
of the three methods described above.
ANTI-ALIAS FILTER DESIGN Given that we know the maximum unaliased frequency fmax at each point along the migration operator, we need to design a method to locally lowpass filter the seismic data in order to satisfy the anti-aliasing criterion (1). We implement the local lowpass filters as triangular smoothing. The Z-transform representation of an arbitrary N-point triangle filter can be expressed as
| |
(9) |
where the triangle length N = 2k+1, and the filter scaling
coefficient ![]() . The amplitude spectrum of the
triangle filter can be derived as
. The amplitude spectrum of the
triangle filter can be derived as
| |
(10) |
which is the discrete version of a continuous sinc2 function, and has spectral notches at the frequencies
| |
(11) |
We design the triangle filter length N such that the maximum unaliased frequency fmax is equal to the first notch in the triangle spectrum at frequency f1. Equating the anti-aliasing criterion (1) to the first triangle filter notch frequency of (11), we derive the appropriate anti-aliasing triangle filter length N to be
| |
(12) |
The value of the local migration operator dip ![]() is given
by equation (4) in the case of time migration, or by the methods
discussed in the previous section on depth migration.
is given
by equation (4) in the case of time migration, or by the methods
discussed in the previous section on depth migration.
Furthermore, we note that the denominator of g(z) represents a causal integration of the trace with 1/(1-z), followed by an anticausal trace integration with 1/(1-z-1). The numerator of g(z) is a gapped three-point Laplacian operator, where the length of the gap (k+1) determines the triangle length N and high-cut frequency fmax. Therefore, if the input trace data are integrated twice before migration, an arbitrary N-point anti-alias triangle filter can be designed and applied on the fly for the cost of a three-point operator. This observation offers a large savings in computational effort when applying the triangle filters.
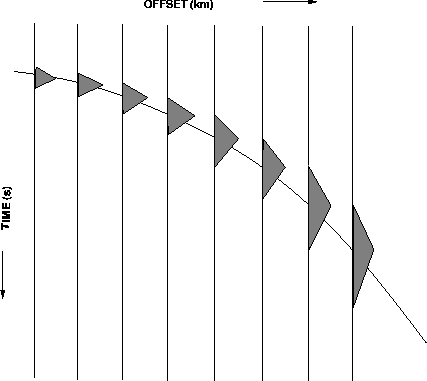
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a schematic diagram of a migration
impulse response filtered with the anti-aliasing triangles.
The triangle filters get longer with increasing operator dip in
order to suppress aliasing of high temporal frequencies.
The peak amplitude of the triangle should decrease as the filter
length increases according to the factor
shows a schematic diagram of a migration
impulse response filtered with the anti-aliasing triangles.
The triangle filters get longer with increasing operator dip in
order to suppress aliasing of high temporal frequencies.
The peak amplitude of the triangle should decrease as the filter
length increases according to the factor ![]() in Equation (9),
but this is not shown in the diagram of Figure
in Equation (9),
but this is not shown in the diagram of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |
DATA EXAMPLES
We compare examples of standard Kirchhoff migration with our
anti-aliased migration method. Standard migration is defined
here as Kirchhoff migration with a ![]() operator dip filter
and a 45-degree migration aperture. The anti-aliased migration
is a full-aperture migration with no operator dip-filtering except
as supplied by the anti-aliasing triangle filters.
operator dip filter
and a 45-degree migration aperture. The anti-aliased migration
is a full-aperture migration with no operator dip-filtering except
as supplied by the anti-aliasing triangle filters.
Zero-dip migration aliasing
The first example illustrates the method in the absence of
data aliasing. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a stacked section from
offshore Florida which exhibits a strong bottom simulating reflection
(BSR) due to the presence of a frozen methane-hydrate layer overlaying
a free-methane gas-saturated layer. The deepwater seafloor reflection,
the BSR and the flat spot at the base of the free-gas layer are labeled.
This data is the subject of an AVO analysis by Ecker and Lumley (1993a,
1993b, 1994). The stacked section clearly shows that the geologic structure
is near zero-dip, and therefore the prestack data are not likely to
suffer from much spatial data-aliasing.
shows a stacked section from
offshore Florida which exhibits a strong bottom simulating reflection
(BSR) due to the presence of a frozen methane-hydrate layer overlaying
a free-methane gas-saturated layer. The deepwater seafloor reflection,
the BSR and the flat spot at the base of the free-gas layer are labeled.
This data is the subject of an AVO analysis by Ecker and Lumley (1993a,
1993b, 1994). The stacked section clearly shows that the geologic structure
is near zero-dip, and therefore the prestack data are not likely to
suffer from much spatial data-aliasing.
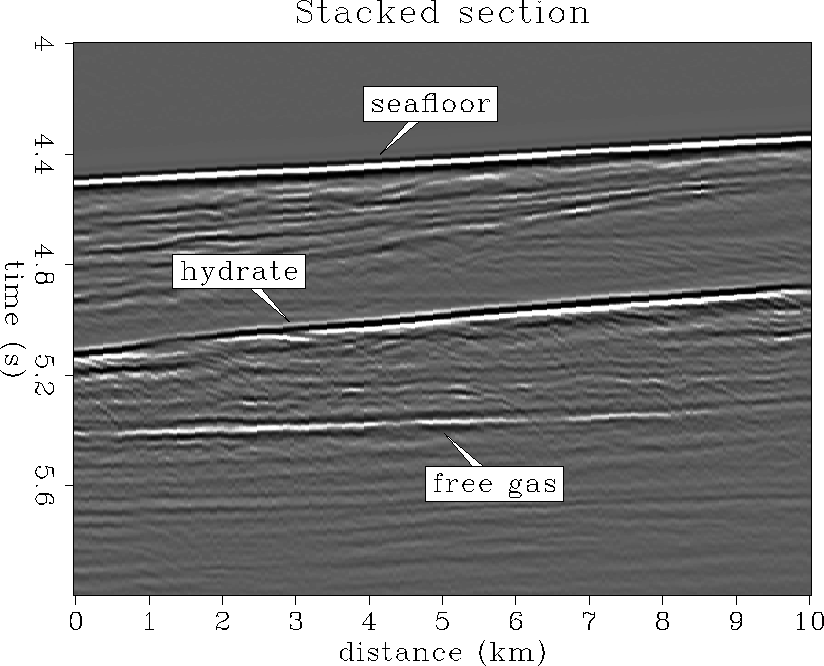 |
Although the data are not aliased, the migration operator certainly is.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a migration ``impulse response'' which is obtained
by migrating ten adjacent prestack traces in a common-offset section
with the standard Kirchhoff method defined above.
Note the severe checkerboard ``speckling'' along
steep parts of the migration responses which is a common indicator of
operator aliasing. Although the structure is nearly horizontal and
the data are not aliased, the migration operator is aliased because
the migration velocity is low (water), and the trace spacing is
fairly coarse at 50 m interval sampling. Low migration velocity
and coarse trace spacings conspire to reduce the maximum temporal frequency
that remains unaliased along steep operator dips, as related by
Equation (8).
Figure
shows a migration ``impulse response'' which is obtained
by migrating ten adjacent prestack traces in a common-offset section
with the standard Kirchhoff method defined above.
Note the severe checkerboard ``speckling'' along
steep parts of the migration responses which is a common indicator of
operator aliasing. Although the structure is nearly horizontal and
the data are not aliased, the migration operator is aliased because
the migration velocity is low (water), and the trace spacing is
fairly coarse at 50 m interval sampling. Low migration velocity
and coarse trace spacings conspire to reduce the maximum temporal frequency
that remains unaliased along steep operator dips, as related by
Equation (8).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the migration result using our
operator anti-aliasing method instead of standard operator aperture-control and
dip-filtering. Nearly all of the aliased speckling has been correctly
suppressed.
shows the migration result using our
operator anti-aliasing method instead of standard operator aperture-control and
dip-filtering. Nearly all of the aliased speckling has been correctly
suppressed.
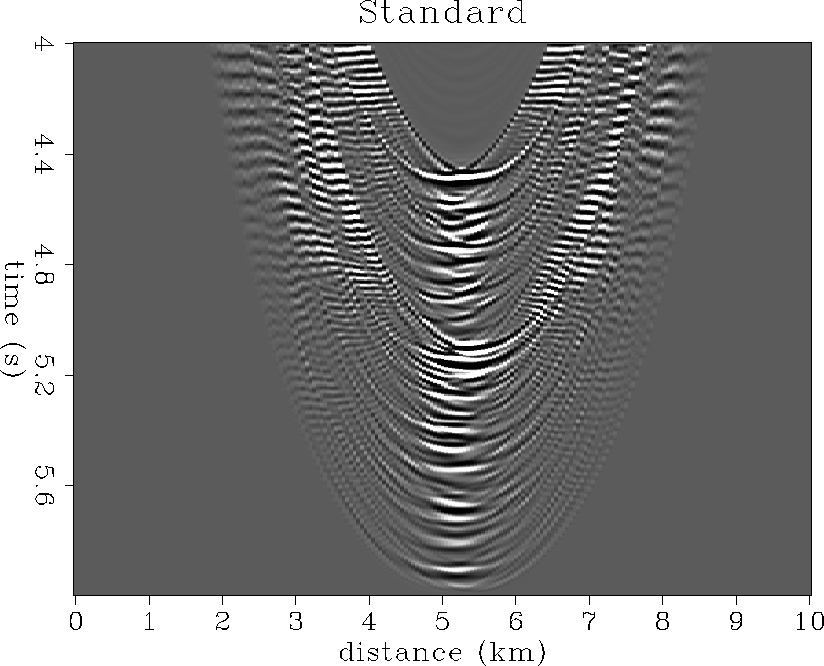 |
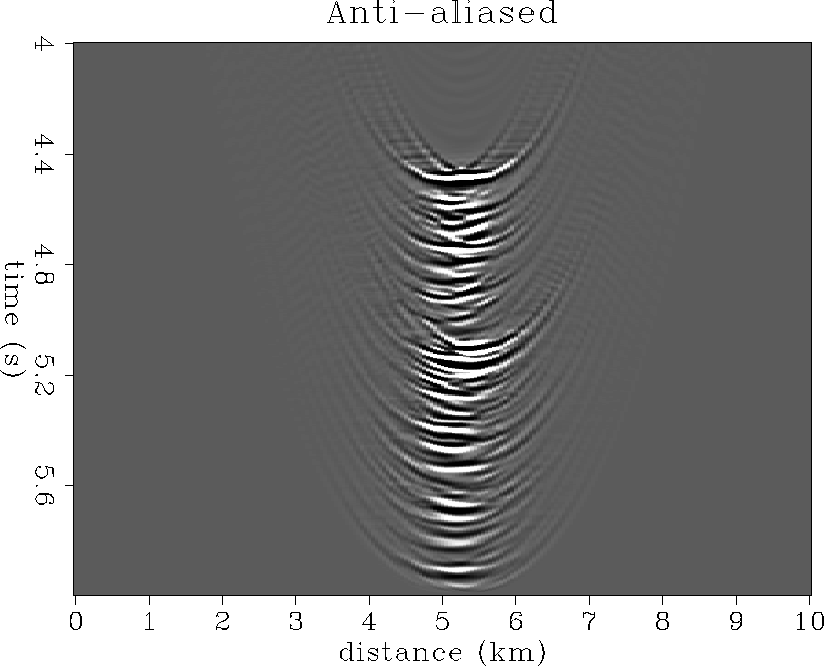 |
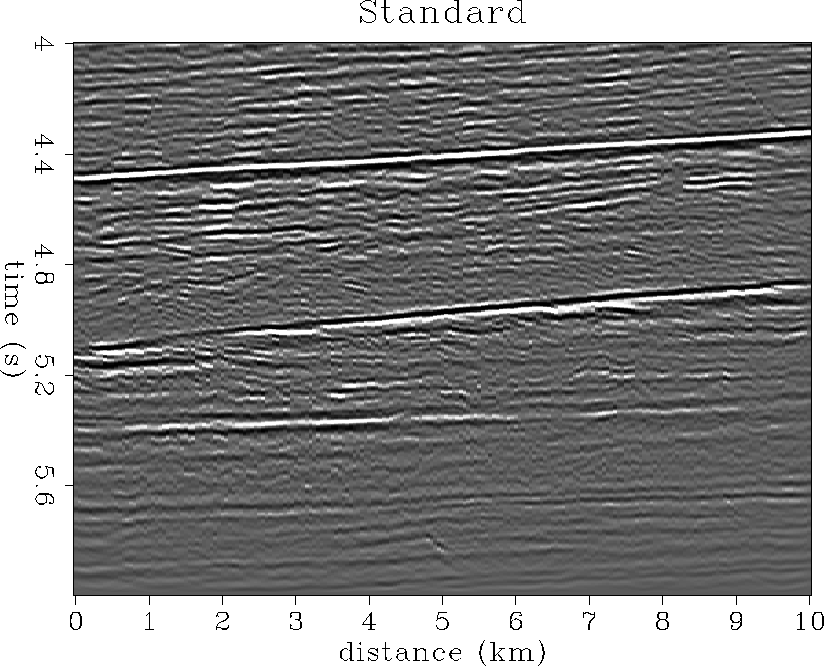
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a common-offset migration using the standard
Kirchhoff method. In comparison to the stacked section of
Figure
shows a common-offset migration using the standard
Kirchhoff method. In comparison to the stacked section of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , many artifacts of operator aliasing are evident.
Especially noteworthy is the fact that the zone above the seafloor
has been severely contaminated by aliasing artifacts that give the
appearance of false reflectivity structure within the seawater!
Additionally, the region between the seafloor and the BSR
has been contaminated, but in a more surreptitious manner.
Figure
, many artifacts of operator aliasing are evident.
Especially noteworthy is the fact that the zone above the seafloor
has been severely contaminated by aliasing artifacts that give the
appearance of false reflectivity structure within the seawater!
Additionally, the region between the seafloor and the BSR
has been contaminated, but in a more surreptitious manner.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the same migration using our anti-aliasing method.
Note that the seawater artifacts have been suppressed and the structure
between the seafloor and the BSR has a clear image.
shows the same migration using our anti-aliasing method.
Note that the seawater artifacts have been suppressed and the structure
between the seafloor and the BSR has a clear image.
 |
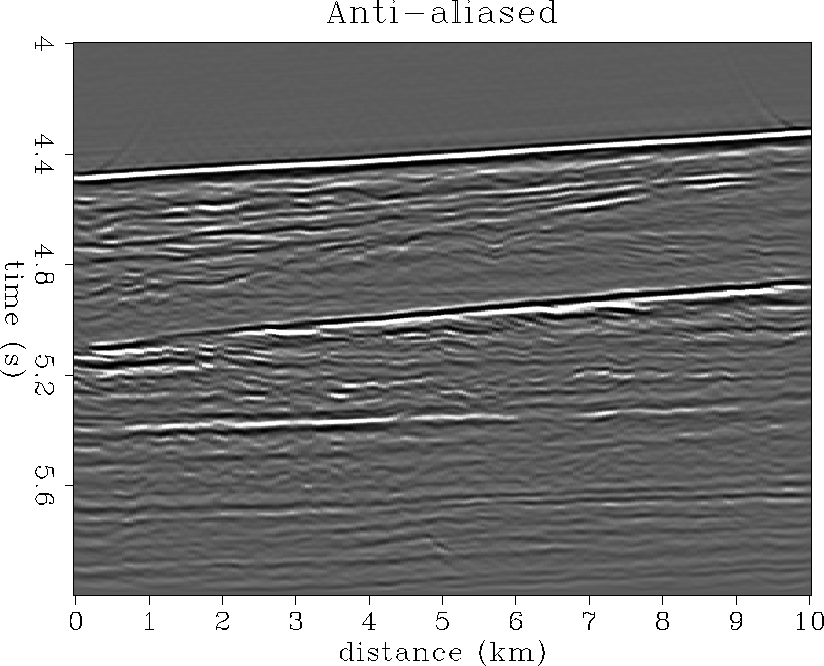 |
3-D anti-aliased migration We now compare our anti-aliased Kirchhoff migration to a conventional aperture-weighted Kirchhoff migration, both implemented on a Connection Machine CM-5. Preliminary 3-D results were shown at the SEG 3-D workshop by Lumley and Claerbout (1993).
The input data approximately represent a 10 km by 10 km surface stack area. The stacked data were decimated to a 50 m by 50 m bin sampling interval in the inline and crossline directions for the purposes of this study. Normally, for the steep dips present on near-vertical faults and salt boundaries, this data would require oversampling by at least a factor of 16 to help suppress aliasing in the migrated image, which is an expensive and possibly prohibitive multiplier. We note that, although these migrations are only 3-D poststack time migrations, the effects of anti-aliasing in the images are dramatic. The anti-aliasing improvements are expected to be even more dramatic for both poststack depth and prestack time/depth migration.
Inline sections
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show inline sections sliced from
the standard and anti-aliased 3-D migration cubes. The crossline position
of these inline sections is at y = 3.7 km. Due to the sparse
sampling of the surface stacked trace bins, the standard migration
is severely aliased, even with the 45 degree migration aperture and
show inline sections sliced from
the standard and anti-aliased 3-D migration cubes. The crossline position
of these inline sections is at y = 3.7 km. Due to the sparse
sampling of the surface stacked trace bins, the standard migration
is severely aliased, even with the 45 degree migration aperture and
![]() operator dip filtering.
Our anti-aliased image is much clearer, and shows a package of
sediments faulted in the center by underlying salt which is pushing upwards.
Figures
operator dip filtering.
Our anti-aliased image is much clearer, and shows a package of
sediments faulted in the center by underlying salt which is pushing upwards.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show inline sections sliced from
the standard and anti-aliased 3-D migration cubes. The crossline position
of these inline sections is at y = 6.15 km.
Again, our anti-aliased migration is superior, and clearly images
a heavily faulted (2 sec) and folded (3 sec) package of sediments
cradled in an arm of the salt body which synclines at 3 km inline distance.
show inline sections sliced from
the standard and anti-aliased 3-D migration cubes. The crossline position
of these inline sections is at y = 6.15 km.
Again, our anti-aliased migration is superior, and clearly images
a heavily faulted (2 sec) and folded (3 sec) package of sediments
cradled in an arm of the salt body which synclines at 3 km inline distance.
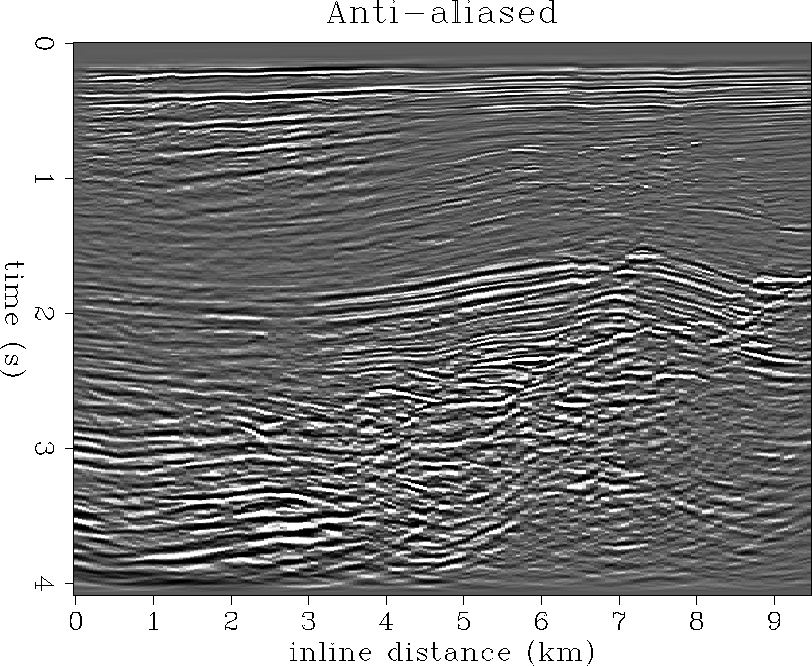
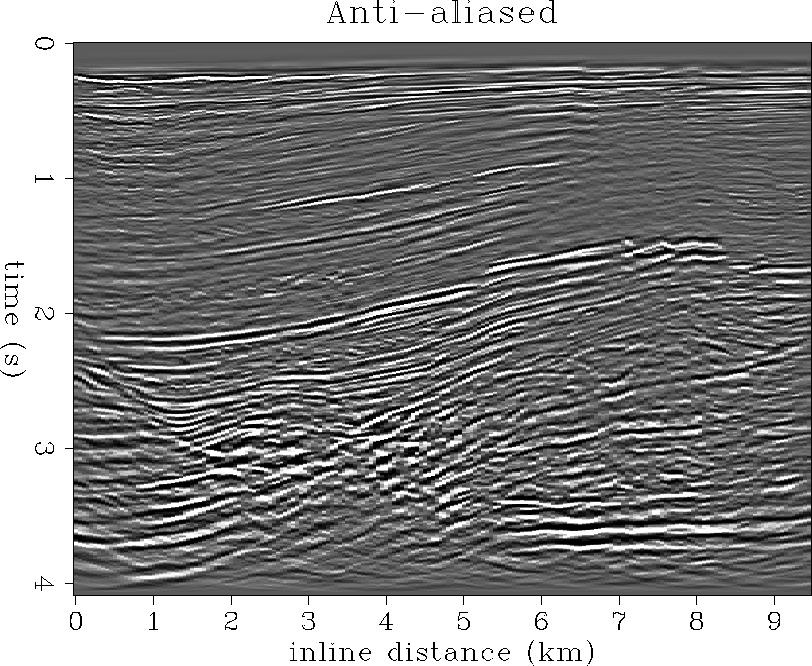
Crossline section
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show crossline sections sliced from
the standard and anti-aliased 3-D migration cubes. The inline position
of these crossline sections is at x=5.5 km. The standard migration
is severely distorted by 3-D migration operator aliasing.
Our anti-aliased migration, however, gives a clear image of the
structure, including an anticlinal sediment package with a large vertical
fault throw at 2 seconds and 6 km crossline distance. The top of
salt is fairly well imaged at the base of the folded sediments.
show crossline sections sliced from
the standard and anti-aliased 3-D migration cubes. The inline position
of these crossline sections is at x=5.5 km. The standard migration
is severely distorted by 3-D migration operator aliasing.
Our anti-aliased migration, however, gives a clear image of the
structure, including an anticlinal sediment package with a large vertical
fault throw at 2 seconds and 6 km crossline distance. The top of
salt is fairly well imaged at the base of the folded sediments.
Time slices
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show time slices cut from
the standard and anti-aliased 3-D migration cubes. The
pseudodepth of each slice is at 1.496 migrated seconds.
This time slice skims the very top of the salt intrusion
body where it first pokes its head up through the deeper sediments.
The edges of the salt body fall almost vertically
down into the deeper sediments. These steep dips are crisply imaged
in the anti-aliased migration, but not visible at all in the
standard migration image. Also, ``waves'' of folded sediments
outline the top of the salt intrusion like ripples around
a piece of floating wood. Nothing discernable is resolved in
the standard migration time slice.
show time slices cut from
the standard and anti-aliased 3-D migration cubes. The
pseudodepth of each slice is at 1.496 migrated seconds.
This time slice skims the very top of the salt intrusion
body where it first pokes its head up through the deeper sediments.
The edges of the salt body fall almost vertically
down into the deeper sediments. These steep dips are crisply imaged
in the anti-aliased migration, but not visible at all in the
standard migration image. Also, ``waves'' of folded sediments
outline the top of the salt intrusion like ripples around
a piece of floating wood. Nothing discernable is resolved in
the standard migration time slice.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show deeper time slices cut from
the standard and anti-aliased 3-D migration cubes. The
pseudodepth of each slice is at 1.744 migrated seconds.
Again, the standard migration image is difficult to interpret.
Our anti-aliased migration, however, clearly shows the intersection
of the salt sediment-cap with the time slice horizon. Note that
the cylindrical shape of the top of salt causes the flanking sediments
to strike at 45 degrees to the acquisition geometry, and the tip of
the salt peninsula causes the anticlinal sediment feature to
the northwest. There is a large fault with about 500 m lateral
throw at (x,y) coordinate (5,6) km, another fault just clipped in
the image at (x,y) coordinate (8.5,8.5) km. Additionally, there
are two vertical faults in the top right corner which bound a set
of steeply-dipping folded sediment layers.
show deeper time slices cut from
the standard and anti-aliased 3-D migration cubes. The
pseudodepth of each slice is at 1.744 migrated seconds.
Again, the standard migration image is difficult to interpret.
Our anti-aliased migration, however, clearly shows the intersection
of the salt sediment-cap with the time slice horizon. Note that
the cylindrical shape of the top of salt causes the flanking sediments
to strike at 45 degrees to the acquisition geometry, and the tip of
the salt peninsula causes the anticlinal sediment feature to
the northwest. There is a large fault with about 500 m lateral
throw at (x,y) coordinate (5,6) km, another fault just clipped in
the image at (x,y) coordinate (8.5,8.5) km. Additionally, there
are two vertical faults in the top right corner which bound a set
of steeply-dipping folded sediment layers.
CONCLUSIONS We have presented an anti-aliasing method for Kirchhoff migration operators, based on local triangle filtering. The N-point triangles are efficiently applied as 3-point filters after causal and anticausal integration of the seismic trace data. This method is well suited for parallel processing algorithms, where storage of multiple copies of various high-cut filtered versions of the input data is often not practical. We compare the anti-aliasing method to a standard Kirchhoff 3-D migration, using a salt intrusion dataset from the Gulf of Mexico. Our results indicate that careful operator anti-aliasing can enhance steep-dip reflections from faults and salt-sediment interfaces during the process of 3-D seismic migration imaging. Our method is applicable to other Kirchhoff space-time operators such as NMO velocity stacking and DMO.
ACKNOWLEDGMENTS
We thank Dave Nichols, Biondo Biondi and Stew Levin for helpful comments on the subject of operator aliasing. Mihai Popovici arranged for Halliburton Geophysical Services to provide the 3-D salt intrusion dataset used in this study.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
REFERENCES
 |
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)