 |
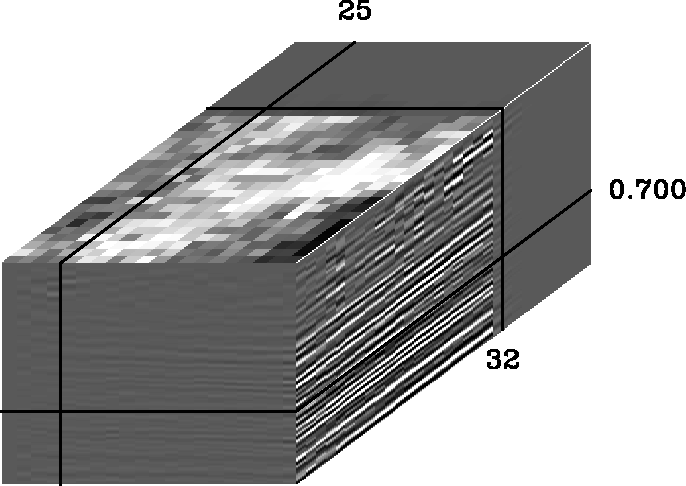
Figure 4 Extrapolation using the concatenation of the results of four directional filters. The poor extrapolation of the data is barely visible.
Each of the four directional filters is calculated separately on the same input data to produce the best prediction possible with its direction. Incorporating these four filters to create a single predicted result may be done in several ways.
One obvious approach would be to merge the four results by windowing out the bad results at the edges and averaging the results in the center. The problem with this approach is that the poor predictions extend well into the data when a filter cannot predict a particular dip. Averaging the four results simply weakens the best prediction.
Another approach is to minimize a concatenation of f1 * d, f2 * d, f3 *d, and f4 * d, where the fs are the filters, d is the original plus the extrapolated data, and * indicates three-dimensional convolution. Oddly enough, this produced the very poor prediction seen in Figure 4. Originally, this poor prediction appeared to be a program error, but it may be the result of no single result satisfying all four prediction requirements.
 |
 |
An alternative to the simultaneous minimization of all four results is the minimization of the sum of the results, that is, minimizing f1 * d + f2 * d + f3 *d + f4 * d. This approach appears to produce good results without significant edge effects. The results of this extrapolation are shown in Figure 5. The edge effects have been eliminated and the data have been extrapolated as far as in Figure 3. The quality of the results may be considered surprising, since it might be imagined that the sum of the predictions might work against each other to produce large errors.
While the elimination of the edge effects is still not well understood, a possible explanation is that three of the four filter actions may be ignored, while the filter with the best prediction action extrapolates the data. Bad predictions from the weaker filters are suppressed. Another way of thinking about the result is that the central part of the volume is predicted by a combination of the four filters that can be considered as a single filter with coefficients in all directions. At the edges of the volume, only one or two filters contribute to the output, but these filters do not create bad edge effects. There may be some scaling problems at the edges where changes to the number of contributing filters occur, but I have not yet had the opportunity to investigate this.