RESULTS AND BOUNDARY CONDITIONS

Figure 1 was made with a $3\times 3\times 3$ filter.

 

fullcube
Figure 1 Original cube on left. The back half of the cube was chopped off. Right shows the reconstruction. Press button for X11movie.

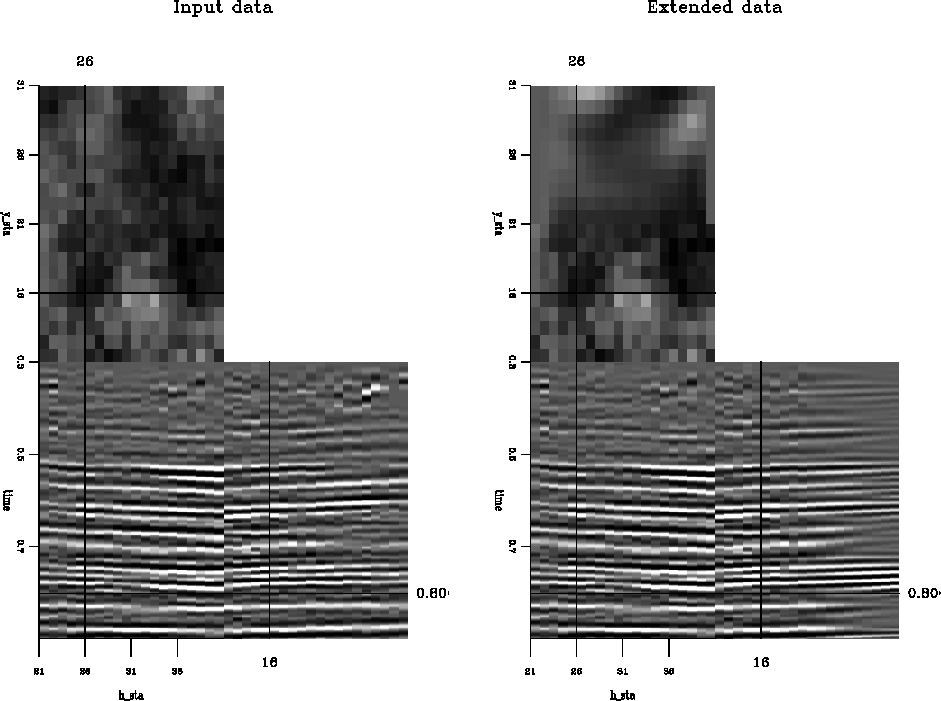Looking at movies I got a better idea of the quality of the extension than you will be able to get from looking at the paper figure. I believe it is fair to say that the extended cube is generally more pleasing than it appears on the paper copy. An exception is the side boundary planes which are poor, although this also is not clear from the paper figure.

As a last resort, I adjusted the triangle windows to match the outputs of a PE filter instead of the input data. Even this is not a satisfactory solution, as careful inspection, not apparent on the given figure, shows that the second-from-end side panels are also poorer than expected.

An early decision was made to use side boundary conditions where the filter does not flow off the data. I call these ``don't care'' or ``internal'' end conditions, although neither name is quite right. Such ends are essential for internal boundaries to be seamless. The boundaries surrounding the entire mass, however, probably should be handled in a different manner because a growing solution at the sides is a likely result. Also, if the data contains large internal gaps, difficulty is likely to arise where patches accidentally cross the gaps. A robust solution to the missing data problem would involve designing subvolume shapes and sizes based on the shapes and sizes of the data gaps. This is beyond my present needs, however. Slow growth with distance is not a problem if you are not planning to extrapolate a long distance. I believe that the extrapolation of the 3-axis in Figure 1 is growing slowly with distance and that this can be controlled in either of two ways: (1) using a different boundary condition, namely, zero value some distance away, or with stabilization. You can experiment with the stabilization that I left switched off in subroutine miss3() . I define stability as the data having finite energy as its volume tends to infinity. Stabilization is certain with an impulsive prior filter, i.e., bb( b1=1, b2=1, b3=1). Other priors have directions that they extrapolate data in a stable manner. With ``don't care'' or ``internal'' end conditions, I believe the only filter that assures stability for data volume expansion in all directions is the impulse function.