The simplest possible interpolation scheme would be to assume that
the Green's function could be modeled as a single, non-dispersive,
zero phase event. It would then be characterized by an amplitude,
A(x,z) and frequency independent traveltime ![]() . To estimate
these two parameters we only need the Green's function calculated at
one frequency,
. To estimate
these two parameters we only need the Green's function calculated at
one frequency,![]() . The amplitude is assumed
to be the same for all frequencies and the traveltime is simply
given by the unwrapped phase divided by the frequency,
. The amplitude is assumed
to be the same for all frequencies and the traveltime is simply
given by the unwrapped phase divided by the frequency, ![]() . The Green's function for all
frequencies is then given by,
. The Green's function for all
frequencies is then given by, ![]() . This simple scheme has little advantage over eikonal
equation based methods. It uses the same simple model for the
Green's function, it does have the advantage of using a calculation in
the seismic data bandwidth (rather than at infinite frequency) but
it has the disadvantage that it breaks down rapidly in the presence
of multiple events.
. This simple scheme has little advantage over eikonal
equation based methods. It uses the same simple model for the
Green's function, it does have the advantage of using a calculation in
the seismic data bandwidth (rather than at infinite frequency) but
it has the disadvantage that it breaks down rapidly in the presence
of multiple events.
The next simplest method will also fail in the presence of multiple
arrivals but it provides a more general model of the event. This
model assumes that both the amplitude and phase are linear functions
of frequency over some bandwidth ![]() . Within this band the Green's function can be modeled by an
initial amplitude and phase, and an amplitude and phase gradient.
Two Green's functions at frequencies
. Within this band the Green's function can be modeled by an
initial amplitude and phase, and an amplitude and phase gradient.
Two Green's functions at frequencies ![]() and
and ![]() are
required to fit this model,
are
required to fit this model,
 |
(1) | |
| (2) | ||
| (3) | ||
| (4) |
The Greens function at any frequency within this band can then be calculated by,
 |
(5) | |
| (6) | ||
| (7) |
This model allows the event to have a constant phase shift (as expected for overturned waves ) and for amplitude to vary as a function of frequency. If this model is used piecewise within the seismic bandwidth it can also be used to model a weakly dispersive event.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a time slice through the Greens'
function for the same velocity gradient medium used earlier.
Three mono-frequency Green's functions were calculated and used to
estimate all the frequencies. The time slices were generated by applying an
inverse FFT. The expanding wavefront has
overturned waves near the top of the section. Figure
shows a time slice through the Greens'
function for the same velocity gradient medium used earlier.
Three mono-frequency Green's functions were calculated and used to
estimate all the frequencies. The time slices were generated by applying an
inverse FFT. The expanding wavefront has
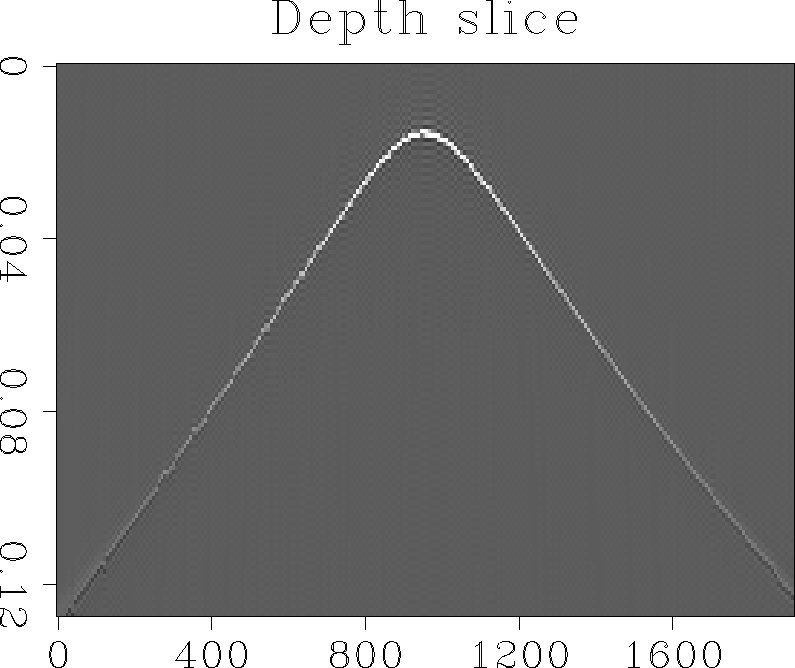
overturned waves near the top of the section. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a depth slice through the Green's function. The phase changes on
the limbs of the hyperbola correspond to the point at which the
waves overturn. It is encouraging that
all the major features expected in this Green's function have been
recovered from an extrapolation of only three frequencies.
shows a depth slice through the Green's function. The phase changes on
the limbs of the hyperbola correspond to the point at which the
waves overturn. It is encouraging that
all the major features expected in this Green's function have been
recovered from an extrapolation of only three frequencies.
 |
 |
When there are multiple arrivals at a particular location both of these simple interpolation methods will fail. In this situation an interpolation scheme based on a multiple event model must be used. This is a subject for future research, I will not discuss it further in this paper.