In an earlier paper I described a method for calculating
mono-frequency Green's functions by using one-way equations in a
polar coordinate frame. This method has the advantage that high
dips can be correctly modeled using a paraxial operator. I use a
![]() extrapolation operator which will accurately model waves
propagating at up to
extrapolation operator which will accurately model waves
propagating at up to ![]() to the polar coordinate grid.
These waves may be traveling at much higher angles to the the
rectangular coordinate frame and may even be propagating at
angles greater than
to the polar coordinate grid.
These waves may be traveling at much higher angles to the the
rectangular coordinate frame and may even be propagating at
angles greater than ![]() (overturned waves).
(overturned waves).
The 2-D polar coordinate wave equation,
![]()
![\begin{displaymath}
\frac{\partial P} {\partial r } =\left( \frac{-1}{r^2} + i \...
...alpha}{4r^2} \frac{\partial^2}{\partial \theta^2 } }\right] P
\end{displaymath}](img6.gif)
![]()
This equation can be used for outward extrapolation of a single
frequency from some initial radius r0, to give a solution on the
whole ![]() plane. The initial solution at r=r0 is the
solution for a homegenous medium.I choose to express this solution
in terms of amplitude and wrapped phase,
plane. The initial solution at r=r0 is the
solution for a homegenous medium.I choose to express this solution
in terms of amplitude and wrapped phase, ![]() and
and
![]() . Starting from the known phase at r=r0
I perform a phase unwrapping to obtain the unwrapped phase
. Starting from the known phase at r=r0
I perform a phase unwrapping to obtain the unwrapped phase
![]() . The amplitude and phase are then mapped
back to the rectangular coordinate frame using a simple bilinear
interpolation.
. The amplitude and phase are then mapped
back to the rectangular coordinate frame using a simple bilinear
interpolation.
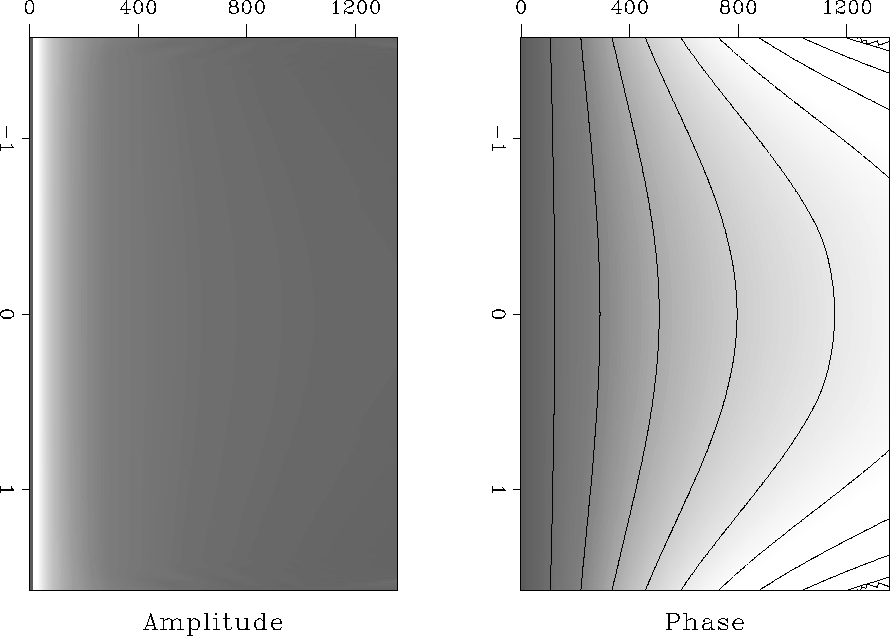
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the amplitude and unwrapped phase
for a polar coordinate Green's function in a medium with velocity
that is a linear function of depth. Figure
shows the amplitude and unwrapped phase
for a polar coordinate Green's function in a medium with velocity
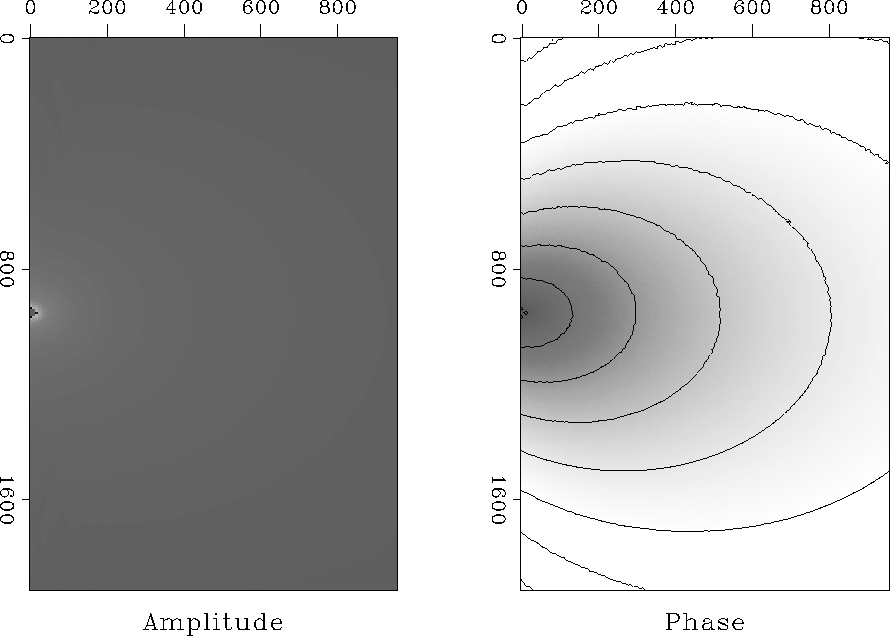
that is a linear function of depth. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
the same Green's function mapped back to rectangular coordinates.
shows
the same Green's function mapped back to rectangular coordinates.
 |
 |
All of these calculations are done in parallel for a number of frequencies. If all the frequencies are calculated we then have a complete Green's function. However, calculating all the frequencies can be very expensive so I only calculate a limited number. The missing frequencies must then be estimated from the ones calculated.