




Next: Sets of equations and
Up: DERIVING THE SYSTEM OF
Previous: Time relationships in the
At the reflector point R, the ray must obey Snell's law. In other words,
the angle of incidence must equal the angle of reflection. In terms of
ray paths, 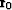 fixes the position of the reflection plane,
and
fixes the position of the reflection plane,
and 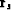 and
and 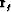 account for the angles of incidence and
reflection. Since
account for the angles of incidence and
reflection. Since 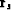 and
and 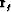 have equal lengths
1/v, Snell's law can be expressed in the following vectorial form:
have equal lengths
1/v, Snell's law can be expressed in the following vectorial form:
| 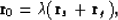 |
(9) |
where 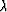 is a coefficient of proportionality. The first
two coordinates are the ray parameter components, which have
the following relation:
is a coefficient of proportionality. The first
two coordinates are the ray parameter components, which have
the following relation:
| 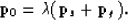 |
(10) |
The third coordinate of the ray path vectors can be expressed
as a function of the inclination angle and the vector length,
1/v, as follows:
| 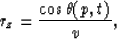 |
(11) |
where 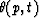 is the table of angles along a ray of
parameter p and time t. Then, after simplification of
the 1/v factors (the velocity is the same for all rays
at the reflector point), the third equation of
relation (9) becomes
is the table of angles along a ray of
parameter p and time t. Then, after simplification of
the 1/v factors (the velocity is the same for all rays
at the reflector point), the third equation of
relation (9) becomes
| 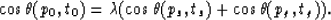 |
(12) |
Substituting equation (12) into relation (10),
we can eliminate the proportionality factor 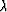 to obtain
the following relation:
to obtain
the following relation:
| 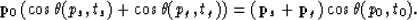 |
(13) |





Next: Sets of equations and
Up: DERIVING THE SYSTEM OF
Previous: Time relationships in the
Stanford Exploration Project
11/17/1997