




Next: APPROXIMATING TI MEDIA WITH
Up: Karrenbach: Relating seismic measurements
Previous: Acknowledgments
- Backus, G. E., 1962, Long-wave anisotropy produced by horizontal layering: J. Geophys. Res., 66, 4427-4440.
-
- Dellinger, J., and Muir, F., 1993, Dix revisited : A formalism for rays in layered media: Fifth international workshop on seismic anisotropy, Canadian Soc. Expl. Geophys., Proceedings of the Fifth International Workshop on Seismic Anisotropy.
-
- Dellinger, J., Muir, F., and Karrenbach, M., 1993, Anelliptic approximations for TI media: Journal of Seismic Exploration, 2, 23-40.
-
- Folstad, P. G., and Schoenberg, M., 1992, Use of equivalent anisotropic medium theory to calculate synthetic seismograms: SEG Summer Research Workshop on AVO, Soc. Expl. Geophys., Expanded Abstracts.
-
- Kennett, B. L. N., 1974, Reflections, rays and reverberations: Bull. Seis. Soc. Am., 64, 1685-1696.
-
- Muir, F., 1991, Various equations for transverse isotropic media: SEP-70, 367-372.
-
- Nichols, D., and Karrenbach, M., 1990, What is equivalent in an equivalent medium ?: SEP-67, 1-4.
-
- Schoenberg, M., and Muir, F., 1989, A calculus for finely layered anisotropic media: Geophysics, 54, no. 5, 581-589.
-
Following Francis Muir's notation, I use the following symbols:
Wij is 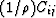 , an elastic modulus divided by density;
C is
, an elastic modulus divided by density;
C is 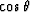 and
S is
and
S is  .More detailed and complete definitions for all wave types can be found in
Muir (1991).
.More detailed and complete definitions for all wave types can be found in
Muir (1991).
Stanford Exploration Project
11/17/1997
![]() , an elastic modulus divided by density;
C is
, an elastic modulus divided by density;
C is ![]() and
S is
and
S is ![]() .More detailed and complete definitions for all wave types can be found in
Muir (1991).
.More detailed and complete definitions for all wave types can be found in
Muir (1991).