|
syngeometry
Figure 1 Synthetic surface recording geometry. solid squares represent geophone location on an undulating surface. |  |
|
syngeometry
Figure 1 Synthetic surface recording geometry. solid squares represent geophone location on an undulating surface. |  |
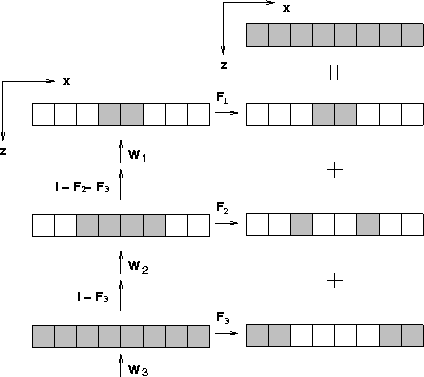
Figure 2 schematically describes the forward modeling algorithm for the simple model. Wi represents upward extrapolation at the i-th depth level and F1, F2, and F3 are spatial filters for grabbing the wavefield where the geophones are located at the corresponding depth levels. The operators I-F3 and I-F2-F3 in Figure 2 stop the wavefield at the locations where it is recorded below or at the corresponding depth level and pass the wavefield at the locations where it is not yet recorded. Each small rectangle in Figure 2 represents an abstract vector that contains wavefields at the corresponding space location. The wavefield along the irregular surface is obtained by summing the wavefields that are grabbed at the various depth levels.
 |
The forward modeling scheme shown in Figure 2 can be algebraically generalized, if we divide the topography into z levels, as follows:
| (1) |
| (2) |
| (3) |
In equation (1), d0 and dz are wavefields on the irregular surface and the datum level, respectively. The extrapolation operator E is followed by the spatial filter G at every depth level. We can see that the upward extrapolation operator Wi is applied to the wavefield that does not arrived at the surface because the operator Ki-1 remove the wavefield if it has arrived at any previous depth level. All wavefields that arrive at the surface are saved by the operator Fi-1 for the final output. For the simple geometry shown in Figure 1, F1, F2, and F3 are just diagonal matrices whose elements are 1 where the geophones are located and elsewhere. Thus their diagonal elements are as follows:
![\begin{eqnarraystar}
diag(F_1) & = & \left[ \begin{array}
{cccccccc} 0&0&0&1&1&0...
...n{array}
{cccccccc} 1&1&0&0&0&0&1&1\\ \end{array} \right] \\ \end{eqnarraystar}](img5.gif) |
||