The theory underlying this study is more fully discussed in
Lumley and Beydoun (1991) and Lumley (1993).
I assume a forward model for a ``generalized'' PP reflectivity,
![]() , which combines elements of plane wave reflection
and Rayleigh-Sommerfeld diffraction theory.
I define a differential volume element of
, which combines elements of plane wave reflection
and Rayleigh-Sommerfeld diffraction theory.
I define a differential volume element of ![]() as
as
| |
(1) |
for ![]() , and zero otherwise.
Here, w is angular frequency,
, and zero otherwise.
Here, w is angular frequency, ![]() is compressional velocity,
is compressional velocity,
![]() is the Zoeppritz PP plane wave reflection coefficient
and
is the Zoeppritz PP plane wave reflection coefficient
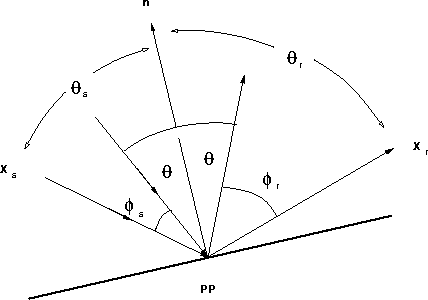
and ![]() (
(![]() ) is the
angle between the incident source (receiver) ray and the specular
ray in Figure
) is the
angle between the incident source (receiver) ray and the specular
ray in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
. ![]() is the specular angle of reflection.
Equation (1) can be integrated over the subsurface volume to model
the reflected scalar wavefield:
is the specular angle of reflection.
Equation (1) can be integrated over the subsurface volume to model
the reflected scalar wavefield:
| |
(2) |
where ![]() (
(![]() ) is the shot (receiver) coordinate, and
) is the shot (receiver) coordinate, and ![]() is
the total traveltime from source to reflection point to receiver.
As (Ar)
is the WKBJ amplitude factor along the source (receiver) leg of the
raypath to the subsurface reflection point
is
the total traveltime from source to reflection point to receiver.
As (Ar)
is the WKBJ amplitude factor along the source (receiver) leg of the
raypath to the subsurface reflection point ![]() , and incorporates the
amplitude effects of source (receiver) directivity, geometric spreading,
transmission loss, and intrinsic high-frequency Q attenuation.
All of these quantities are obtained by raytracing through the
background migration velocity model.
, and incorporates the
amplitude effects of source (receiver) directivity, geometric spreading,
transmission loss, and intrinsic high-frequency Q attenuation.
All of these quantities are obtained by raytracing through the
background migration velocity model.
 |