Nearest neighbor in time and space

In this method I account for the fact that both time and space are discretely sampled. Figure  shows the region subdivided into cells. Within each cell the function value is approximated by the value closest to the center of the cell.

The integral within a cell for this approximation is given by,

$$\int_{\xi_0}^{\xi_1} \tilde{f}( ix, it ) dx = \tilde{f}(ix,it) ( \xi_1 - \xi_0 )$$

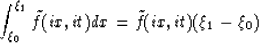
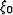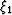where $\xi_0$ and $\xi_1$ are the space coordinates at which the path enters and leaves the cell. The integral along the whole path is the summation of a set of constant values weighted by the width of the path that lies within each cell (for a space integral.)

 

nnt-nns
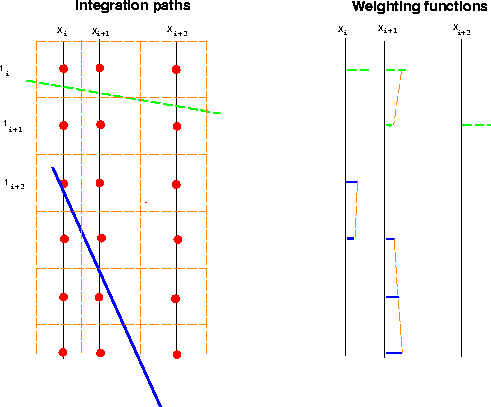
Figure 6 Nearest neighbor is space and time. The function is approximated by a constant value in each cell. The weighting function is the path width within the cell.

A cell is bounded by planes midway between the sample points. There are three types of path through a cell.

1.

When the integration path is near horizontal, it will lie completely within one cell, the sample within that cell will then be scaled by the width of the cell.

2.

If the path passes completely through a cell from top to bottom, the sample will be weighted by the width of the path within that cell. This width can be calculated from the slope of the path.

3.

There are also cases where the path passes through the corner of a cell. In this case the width of the path within the cell is a function of the point at which it enters the cell and the slope.

These three cases have to be dealt with separately when this method is implemented. Note that because of the corner cases this method is not a rectangular weight function on each sampled trace. The method of rectangles proposed by Claerbout implicitly assumes that the path either passes completely through a cell or misses it altogether.

Figure  shows the approximation to the original function surface that is implied by this method. It is clear that for some integration paths the integral through this surface will be a poor approximation to the true integral.

 

nnxnnt-func
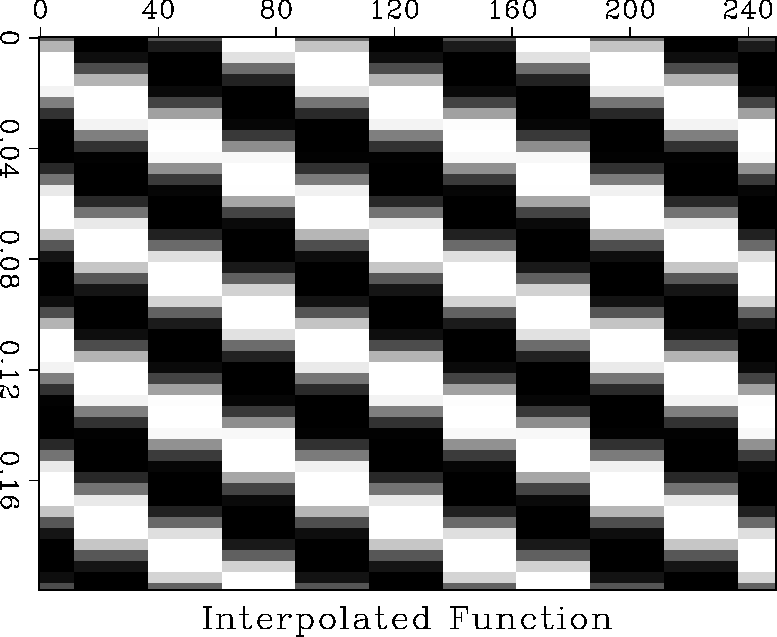
Figure 7 Input data sampled every 4ms in time and 25m in space and then interpolated using nearest neighbor interpolation in space and time.