Using only P-wave phase velocities near the axes

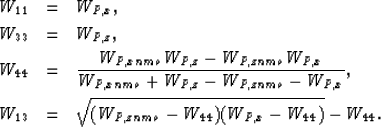
When the medium is TI and no information is available about SV-wave phase velocities, it is still possible to obtain four elastic constants from P-wave phase velocities alone near both axes. This is done by solving the system of equations (4), (5), (13), and (14), which yields:

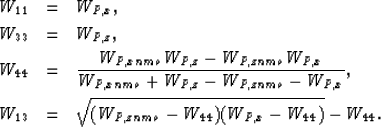$$\begin{eqnarray} W_{11} & = & W_{P,x}, \\ W_{33} & = & W_{P,z}, \\ W_{44} & = & ... ...3} & = & \sqrt{(W_{P,znmo} - W_{44}) (W_{P,x} - W_{44})} - W_{44}.\end{eqnarray}$$ (1) (2) (3) (4)

This set of equations forms the P-wave double elliptic approximation of the elastic constants in a TI medium.

In this approximation, as well as in the previous ones, the assumption of transverse isotropy is crucial. When the medium is isotropic (W_P,x = W_P,z = W_P,xnmo = W_P,znmo) there is no way to calculate W₄₄ (the shear moduli) from P-wave phase velocities alone because equation (24c) is indeterminate. When the medium is weakly anisotropic the estimation of W₄₄ using this approximation may still be unreliable because both the numerator and the denominator in (24c) are close to zero. We will see later in the examples that even when the medium is moderately anisotropic this approximation breaks down quickly for phase angles not close to the axes, unlike the previous vertical and horizontal double elliptic approximations (equations (22) and (23), respectively) that have a wider range a validity.

If only SV-wave phase velocities near the axes are available, it is not possible to obtain the corresponding elastic constants because the system of equations (7), (8), (16), and (17) is underdetermined.