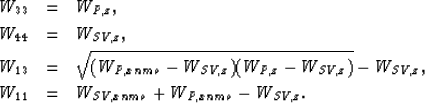
Elastic constants from phase velocities near the vertical.- When the phase angles are close to zero, it is possible to estimate elastic constants from the corresponding phase velocities by using equations (4), (5), (7), and (8), a system of four equations and four unknowns. The independent term (that I haven't explained how to obtain yet) is formed by WP,z, WP,xnmo, WSV,z, and WSV,xnmo. The solution of this system of equations is
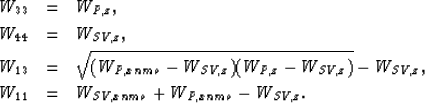 |
(1) | |
| (2) | ||
| (3) | ||
| (4) |
Since this approximation simultaneously uses the elliptical parameters of two ellipses fitted near the vertical, I call it vertical double elliptic approximation, analogous to Muir's double elliptic approximation that uses horizontal and vertical ellipses to approximate the slowness surface and impulse response for all angles (Muir, 1990a; Dellinger et al., 1992). It is important to point out the differences between these two approximations. On the one hand, the vertical double elliptic approximation is used to estimate elastic constants from phase velocities near the vertical axis. Slowness surfaces and impulse responses can be calculated from these elastic constants using (1a) and the exact relationships between phase and group velocities. On the other hand, Muir's double elliptic approximation is used to estimate directly slowness surfaces and impulse responses from data near both axes without having to know the elastic constants.
Fitting P- and SV-wave phase velocities with ellipses near the vertical is not the same as using the vertical double elliptic approximation. However, the fitting is a necessary intermediate step in the estimation of elastic constants using equations (22). When the elliptical fitting is done near the horizontal axis the result is the horizontal double elliptic approximation, as follows.
Elastic constants from phase velocities near the horizontal.- When the phase angle is close to 90 degrees, the expressions for the elastic constants as a function of P- and SV-wave phase velocities are obtained by solving the system of equations (13), (14), (16), and (17), with the following result:
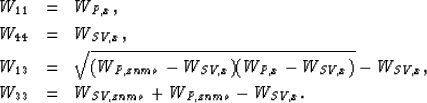 |
(1) | |
| (2) | ||
| (3) | ||
| (4) |
The estimation of W33 from near-horizontal phase velocities (equation (23d)) and W11 from near-vertical phase velocities (equation (22d)) is in both cases the sum of NMO velocities minus W44. Michelena et al. (1992) and Michelena (1992b) show that when estimating velocities tomographically, NMO velocities correspond to the smallest singular values of the problem. The largest singular values correspond to velocities estimated from rays that travel along the axes. Therefore, as expected, estimating W33 from cross-well traveltimes alone is a harder problem than estimating W11 from the same data. The opposite is true when estimating W33 and W11 from VSP measurements.