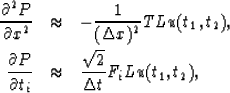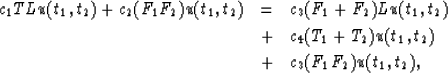Next: IMPULSE RESPONSE
Up: Mujica: Wavefield extrapolation in
Previous: REVIEW OF LITWEQ OPERATOR
Li (1986) presents the finite difference discretization of (7)
with the
diffraction and reverberation terms. He didn't include the second
term at the right hand side of (7), usually called
thin lens term. I am going to show a full LITWEQ discretized operator
using a second order finite difference scheme. This scheme should
be tested with synthetic or real data that has strong lateral
velocity variations to check its stability.
The finite difference scheme uses a nine point star pattern
on (t1,t2). Before the discretization,
we need to define the linear operator
L which represents a convex combination of the
points in the star:
| 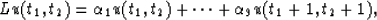 |
(8) |
where u represents the approximate solution to the wave-field. Using
L, the second and first order differential operators can
be approximated as follows:
| 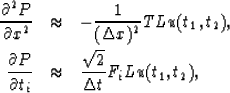 |
(9) |
| (10) |
where T represents the classical centered finite
difference scheme to approximate a second order derivate.
F1 and F2 represent forward schemes to approximate the first order
derivate, along the t1 and t2 respectively.
Substituting (9) and (10) in (7) and approximating the others differential
operators in the conventional way
we get the discretized LITWEQ operator:
| 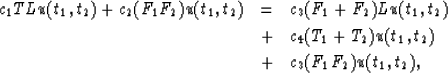 |
|
| |
| (11) |
where ci are functions of 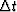 ,
, 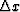 ,
,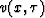 and
and 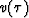 and T1, T2 represent centered schemes along
t1 and t2 respectively.
and T1, T2 represent centered schemes along
t1 and t2 respectively.





Next: IMPULSE RESPONSE
Up: Mujica: Wavefield extrapolation in
Previous: REVIEW OF LITWEQ OPERATOR
Stanford Exploration Project
11/17/1997