UNDERMIGRATION CAUSED BY PARABOLIC APPROXIMATION

Migration is based on the one-way wave equation

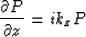$${\partial P\over \partial z} = ik_{z}P$$ (1)

which has the analytic solution

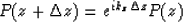$$P(z+\Delta z) = e^{ik_{z}\Delta z} P(z)$$ (2)

where

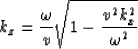$$k_{z} = {\omega \over v} \sqrt { {1-{{v^2k_{x}^2}\over {\omega}^2}}}$$ (3)

and P is the wavefield, z is the depth coordinate, 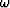$\omega$ is the frequency, v is the velocity, and k_x and k_z are the horizontal and vertical wavenumbers. For small k_x, k_z can be expanded in a series such as

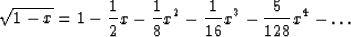$$\sqrt {1-x} = 1 - {1\over 2}x - {1\over 8} x^2 - {1\over 16} x^3 - {5\over 128} x^4 - \ldots$$ (4)

Retaining the first two terms in the expansion results in the 15-degree equation

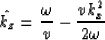$$\hat{k_{z}} = {\omega \over v} -{{vk_{x}^2}\over {2 \omega}}$$ (5)

Because the error term is negative, the approximate 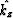$\hat{k_{z}}$ is always greater than the physical k_z. Migration is the process of dephasing (Mo, 1992), which means that, imaging condition (time t=0) is satisfied when the entire exploding reflector upward propagation phase is exhausted. For |k_x|>0, that is, for waves with propagation angles greater than zero, less distance is traveled when the imaging operation is performed. And the larger k_x is, the larger the error term, which results in a smaller propagation distance for the migration response. This explains why the migration impulse response swarms around the vertical axis (Claerbout, 1985, Figure 4.2-2; Yilmaz, 1987, Figure 4-90). Thus the parabolic approximation of the exact one-way wave equation causes undermigration - the specification error. This phenomenon was defined by Claerbout (1985) as anisotropy dispersion.