 |
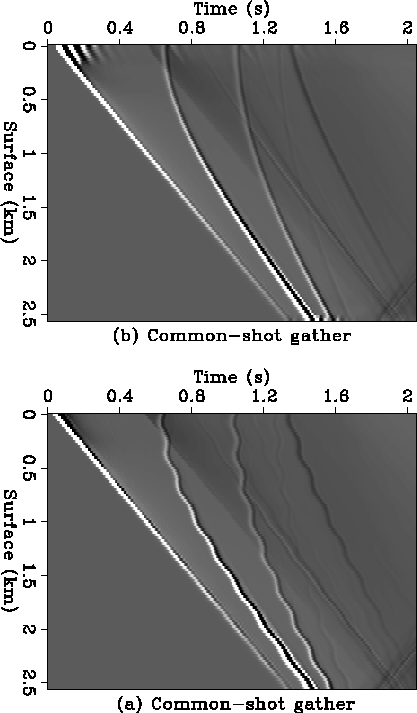
Figure 14 A common-shot gather, (a) recorded on an irregular earth surface showing the raw data without any processing, and (b) with the receivers upward datumed to a planar datum.
I datum correct all the common-shot gathers and common-receiver gathers to a common planar datum just above all the shots and receivers (Dobrin, 1976) by employing the wave equation, using the finite-difference method with the near surface layer velocity, as in conventional static-shift correction. The near surface layer velocity can be obtained by well-shooting and tomographic inversion (Zhu and McMechan, 1988). Using the near surface layer velocity in the datuming avoids generating wild ray bending at the original lower datum surface as in the water bottom in marine survey.
The land surface supposedly has a sinusoidal topography, which is similar to that in the poststack case of Figure 3, with the same spatial oscillation frequency. Figure 14(a) is such a common-shot gather generated by the finite-difference modeling with the shot and receivers located on this topography. The earth model has two reflectors at depth. The land topography seriously distorts the traveltime trajectory of reflection events. With the recorded common-shot gather wavefields as boundary condition, I run the two-way wave equation forward in time to extrapolate the wavefields to a higher planar datum whose elevation equals that of the highest elevation point of the irregular topography. The new common-shot gather is shown in Figure 14(b). The reflection events have been restored to hyperbolas.
Next, the data are sorted into common-receiver gathers with the receivers located on the planar datum and the shots located on the original irregular datum. I also extrapolate the shots to the upper planar datum.
 |