| |
(14) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) reduces to
the first anelliptic form given by equation (
) reduces to
the first anelliptic form given by equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) );
if
);
if ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) reduces
to the original elliptical
form given by equation (
) reduces
to the original elliptical
form given by equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
Following this newer template,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) (the ray equation) becomes
) (the ray equation) becomes
| |
(15) |
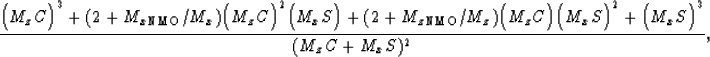
Similarly,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) (the dispersion relation) becomes
) (the dispersion relation) becomes
| |
(16) |
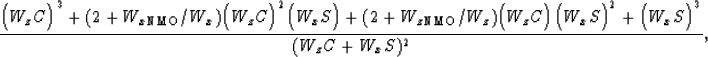
Note that the ![]() subscript indicates
moveout velocity measured for near-vertical propagation; i.e.,
subscript indicates
moveout velocity measured for near-vertical propagation; i.e.,
![]() is the square NMO velocity we use
every day in surface-to-surface data processing.
(If an x subscript seems confusing for a paraxial measurement about
the vertical, remember that in an elliptic world it is a horizontal velocity
that surface moveout measures.)
The
is the square NMO velocity we use
every day in surface-to-surface data processing.
(If an x subscript seems confusing for a paraxial measurement about
the vertical, remember that in an elliptic world it is a horizontal velocity
that surface moveout measures.)
The ![]() subscript indicates
moveout velocity measured for near-horizontal propagation, such
as might be found in a cross-borehole experiment.
subscript indicates
moveout velocity measured for near-horizontal propagation, such
as might be found in a cross-borehole experiment.