




Next: Approximating TI dispersion relations
Up: Dellinger, Muir, & Karrenbach:
Previous: THE SECOND ANELLIPTIC APPROXIMATION
The anelliptic approximations are useful in their own right for
fitting measured phase- and group-velocity surfaces, but it is also
useful to know how to relate these approximations to a real anisotropic
symmetry system. Because the approximations are two-dimensional, the
appropriate symmetry system is transverse isotropy (TI).
The equations for TI media are most easily written in terms of
phase-velocity squared, suggesting we follow the notation of
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
Let 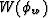 be the phase-velocity squared measured at
phase angle
be the phase-velocity squared measured at
phase angle 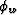 from the vertical, and
let
from the vertical, and
let 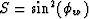 and
and 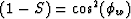 .Express the elastic constants in units of
phase-velocity squared as well, so
.Express the elastic constants in units of
phase-velocity squared as well, so 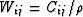 .Then we have for the TI SH wavetype
.Then we have for the TI SH wavetype
| 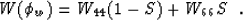 |
(17) |
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is linear because SH waves
in TI media are exactly elliptically anisotropic; by matching coefficients
in equations (
) is linear because SH waves
in TI media are exactly elliptically anisotropic; by matching coefficients
in equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we find
the required anelliptic parameters:
) we find
the required anelliptic parameters:
| 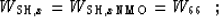 |
(18) |
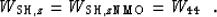
The TI qP-qSV wavetype is rather more complicated:
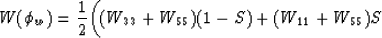
| 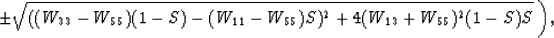 |
(19) |
where the + sign is for qP, - for qSV.
We can find Wz or Wx by substituting S=0
or S=1, respectively, into equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
To find
).
To find 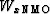 or
or
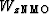 , however,
we first have to fit a paraxial ellipse
about the z or x axes, respectively.
We have already seen that elliptical anisotropy is linear in these coordinates.
To find the equation for the paraxial ellipse about
the z axis we therefore linearize about S=0, obtaining
, however,
we first have to fit a paraxial ellipse
about the z or x axes, respectively.
We have already seen that elliptical anisotropy is linear in these coordinates.
To find the equation for the paraxial ellipse about
the z axis we therefore linearize about S=0, obtaining
| 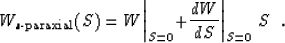 |
(20) |
Next, remembering that 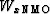 is the horizontal velocity for the paraxial approximation
about the z axis, we set S=1 (horizontal propagation)
in equation (
is the horizontal velocity for the paraxial approximation
about the z axis, we set S=1 (horizontal propagation)
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), obtaining
), obtaining
| 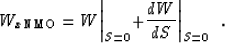 |
(21) |
Similarly,
| 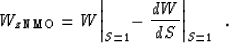 |
(22) |
For the TI qP wavetype we obtain:
| 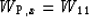 |
(23) |
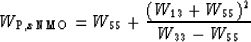
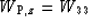
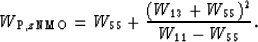
For the TI qSV wavetype we obtain:
| 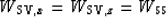 |
(24) |
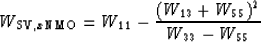
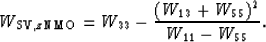





Next: Approximating TI dispersion relations
Up: Dellinger, Muir, & Karrenbach:
Previous: THE SECOND ANELLIPTIC APPROXIMATION
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![]() be the phase-velocity squared measured at
phase angle
be the phase-velocity squared measured at
phase angle ![]() from the vertical, and
let
from the vertical, and
let ![]() and
and ![]() .Express the elastic constants in units of
phase-velocity squared as well, so
.Express the elastic constants in units of
phase-velocity squared as well, so ![]() .Then we have for the TI SH wavetype
.Then we have for the TI SH wavetype
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is linear because SH waves
in TI media are exactly elliptically anisotropic; by matching coefficients
in equations (
) is linear because SH waves
in TI media are exactly elliptically anisotropic; by matching coefficients
in equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we find
the required anelliptic parameters:
) we find
the required anelliptic parameters:
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
To find
).
To find ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), obtaining
), obtaining
![]()
![]()
![]()
![]()
![]()