The $\grave{P}\!\acute{S_1}$ specular reflection coefficient

I now demonstrate the analogous derivation for the $\grave{P}\!\acute{S_1}$ specular reflection coefficient. Again, the least-squares solution is given by (10):

 

$$\grave{P}\!\acute{S_1}({\bf x};{\bf x}_s) = {\bf {\cal R}}_{... ...d^2 \left(\Phi^s_1({\bf x},t)\right)^2\,dt + W_m^2({\bf x})}\;.$$ (38)

For a $\grave{P}\!\acute{S_1}$ reflection, the incident P-wave scalar is the same as (27):

 

$$\Phi^s_1({\bf x},t;{\bf x}_s) = {\bf u}^s{\bf \cdot}{\bf e}_1^s = A_o A_s w_1(t-\tau_s) \;.$$ (39)

However, the reflected S₁-wave scalar needs to be evaluated given (4), (24) and (25):

 

$$\Phi^r_i({\bf x},t;{\bf x}_r) = \u^r{\bf \cdot}{\bf e}_2^r =... ...dot{\u}}\nabla\phi_r){\bf \cdot}{\bf n}'\right]\right\}\,dS'\;.$$ (40)

In deriving (40) I have taken the farfield WKBJ approximation of the displacement vector wavefield gradient and divergence terms given in (30)-(31).

Substituting (39) and (40) into (38) and performing the required t integrations, one obtains

 

$${\bf {\cal R}}_{21}({\bf x}) = P_2 / I_1 \;,$$ (41)

such that

$$\begin{eqnarray} \lefteqn{P_2 = } \nonumber \\ & A_o A_s W_d^2({\bf x},\tau_s) ... ...u}}(t_{sr})\nabla\phi_r){\bf \cdot}{\bf n}'\right]\right\}\,dS'\;.\end{eqnarray}$$ (42)

Now ${\bf \dot{\u}}({\bf x},t_{sr})$ is now evaluated at the total incident P plus reflected S ray traveltime $t_{sr}=\tau_s+\phi_r$. The subscripts on $\lambda_r$ and $\mu_r$ indicate that the Lamé parameters should be evaluated at the receiver positions ${\bf x}_r$, and the $\ast$ symbol still signifies a convolution of the surface data $\u$ with the estimated P-wave source wavelet w₁. The P-wave autocorrelation integral is the same as the $\grave{P}\!\acute{P}$ case:

 

$$I_1 = A_o^2 A_s^2 \int_{t'}W_d^2({\bf x},t') w_1^2(t')\,dt' + W_m^2({\bf x}) \;.$$ (43)

Combining (41)-(43) yields:

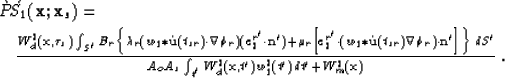$$\begin{eqnarray} \lefteqn{\grave{P}\!\acute{S_1}({\bf x};{\bf x}_s) = } \nonumbe... ...s \int_{t'}W_d^2({\bf x},t') w_1^2(t')\,dt' + W_m^2({\bf x}) } \;.\end{eqnarray}$$ (44)

Equation (44) gives the least-squares elastic wavefield integral solution for $\grave{P}\!\acute{S_1}$ specular reflectivity. It also can be slightly simplified further by noting that

 

$$\nabla\phi_r = {\bf e}_2^{r'} / \beta_r \;,$$ (45)

which follows from the S-wave eikonal equation in (15), where $\beta_r$ is the S-wave velocity evaluated at each receiver position ${\bf x}_r$.